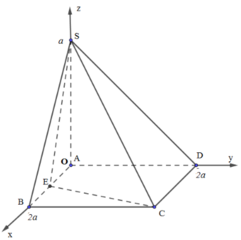
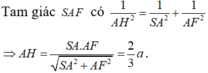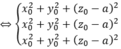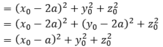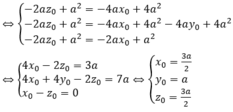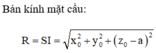Cho hình vuông ABCD có các cạnh bằng a. E; F; G; H lần lượt là trung điểm của các cạnh AB; BC; CD; DA. M là giao của CE và DF
a CM : EFGH là hình vuông
b CM : DF vuông góc với CE và tam giác MAD cân
c Tính diện tích tam giác MDC theo a
MƠN CÁC BẠN NHIỀU