Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
c: Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
a)Nối D với F. Xét \(\Delta BDF\) và \(\Delta FDE\) ta có:
\(\widehat{BDF}=\widehat{DFE}\) (so le trong (Vì AB//EF (gt)))
DF cạnh chung
\(\widehat{DFB}=\widehat{FDE}\) (so le trong (Vì DE//BC (gt)))
\(\Rightarrow\Delta BDF\)\(=\Delta FDE\) (g.c.g)
\(\Rightarrow DB=EF\) (2 cạnh tương ứng )
Mà \(DB=DA\) (D là trung điểm AB)
Suy ra AD=EF
b)Xét \(\Delta ADE\) và \(\Delta EFC\:\) ta có:
\(\widehat{ADE}=\widehat{CFE}\) (\(=\widehat{BAC}\); đồng vị của DE//BC và EF//AB)
\(AD=EF\) (cmt)
\(\widehat{DAE}=\widehat{FEC}\) (đồng vị của DE//BC)
\(\Rightarrow\Delta ADE=\Delta EFC\) (g.c.g)
c)Vì \(\Delta ADE=\Delta EFC\) (cmt)
Suy ra \(AE=EC\) (2 cạnh tương ứng )
Xét Δ DBF và Δ FDE, ta có:
∠(BDF) =∠(DFE) (so le trong vì EF // AB)
DF cạnh chung
∠(DFB) =∠(FDE) (so le trong vì DE // BC)
Suy ra: Δ DFB = Δ FDE(g.c.g) ⇒ DB = EF (hai cạnh tương ứng)
Mà AD = DB (gt)
Vậy: AD = EF
a: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến ứng với cạnh đáy BC
nên AD là đường cao ứng với cạnh BC
Xét ΔEDB vuông tại D và ΔEDC vuông tại D có
ED chung
DB=DC
Do đó: ΔEDB=ΔEDC
Suy ra: EB=EC
b: Xét ΔABE và ΔACE có
AB=AC
AE chung
EB=EC
Do đó: ΔABE=ΔACE
Suy ra: \(\widehat{ABE}=\widehat{ACE}\)
mà \(\widehat{ABE}=90^0\)
nên \(\widehat{ACE}=90^0\)
Xét ΔABF vuông tại B và ΔACG vuông tại C có
AB=AC
\(\widehat{BAF}\) chung
Do đó: ΔABF=ΔACG
Suy ra: AF=AG
Xét ΔAFG có AF=AG
nên ΔAFG cân tại A
c: Xét ΔAGF có
\(\dfrac{AB}{AG}=\dfrac{AC}{AF}\)
Do đó: BC//GF
d: Xét ΔBEG vuông tại B và ΔCEF vuông tại C có
EB=EC
\(\widehat{BEG}=\widehat{CEF}\)
Do đó: ΔBEG=ΔCEF
Suy ra: EG=EF
Ta có: AG=AF
nên A nằm trên đường trung trực của GF\(\left(1\right)\)
Ta có: EG=EF
nên E nằm trên đường trung trực của GF\(\left(2\right)\)
Ta có: MG=MF
nên M nằm trên đường trung trực của GF\(\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra A,E,M thẳng hàng
mà GC cắt BF tại E
nên AM,BF,CG đồng quy
Xét \(\Delta ABC\) có AD=DB;DE//BC nên AE=EC hay E là trung điểm AC
Xét \(\Delta ADE\) và \(\Delta EFC\) có:
\(\left\{{}\begin{matrix}\widehat{DAE}=\widehat{FEC}\\AE=EC\left(cmt\right)\\\widehat{AED}=\widehat{ECF}\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta ADE\) \(=\) \(\Delta EFC\)\(\left(g.c.g\right)\)
Tick hộ nha
Vì AD=BD và d//BC
=> E là trung điểm của AC
=> AE = EC
Vì DE//BC
=> \(\widehat{AED}=\widehat{ECF}\) (2 góc đồng vị)
Vì ÈF//AB
\(\Rightarrow\widehat{DAE}=\widehat{FEC}\) (2 góc đồng vị)
Xét ΔADE và ΔECF có;
\(\widehat{AED}=\widehat{ECF}\) (cmt)
AE = EC
\(\widehat{DAE}=\widehat{FEC}\) (cmt)
=> ΔADE = ΔECF (g-c-g)
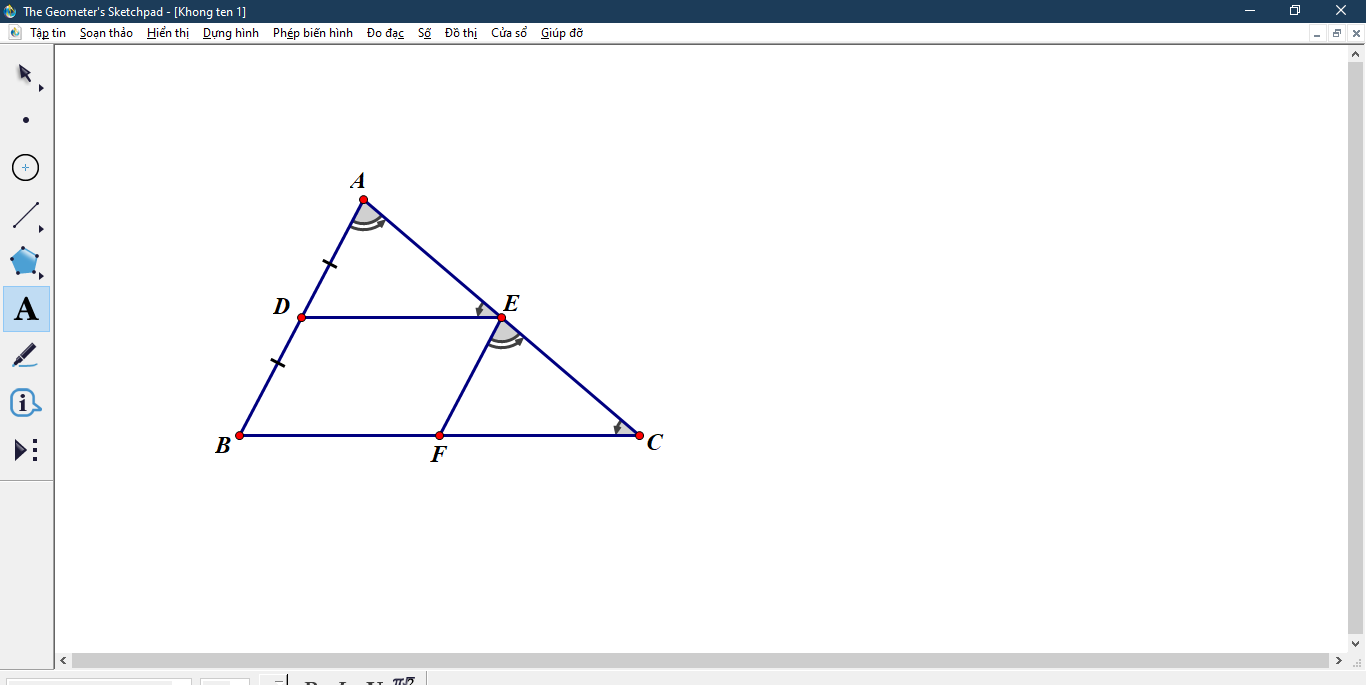
Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và song song với BC cắt AC ở E, đường thẳng qua E và song song với AB cắt BC ở F. Chứng minh rằng :
a) AD = EF
b) Tam giác ADE = Tam giác EFC= tam giác DBF
c) BC= 2 lần DE
D với F. Xét ΔBDF và ΔFDE ta có:
ˆBDF=^DFE (so le trong (Vì AB//EF (gt))
DF cạnh chung
ˆDFB=ˆFDE(so le trong (Vì DE//BC (gt))
⇒ΔBDF=ΔFDE (g.c.g)
⇒DB=EF (2 cạnh tương ứng )
Mà DB=DA (D là trung điểm AB)
Suy ra AD=EF
b)Xét ΔADE và ΔEFC ta có:
ˆADE=ˆCFE (=ˆBAC; đồng vị của DE//BC và EF//AB)
AD=EF (cmt)
ˆDAE=ˆFEC(đồng vị của DE//BC)
⇒ΔADE=ΔEFC (g.c.g)
c)Vì ΔADE=ΔEFC (cmt)
Suy ra AE=EC (2 cạnh tương ứng )
HT
