Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có:
Mà OB ⊥ BC ⇒ IM ⊥ BC
Ta có:
IM ⊥ BC
BC ⋂ (I; IM) = {M}
Suy ra, BC là tiếp tuyến của đường tròn tâm I, bán kính IM
Đường tròn có đường kính BC có tâm M, bán kính MA.OO' vuông góc với MA tại A nên là tiếp tuyến của đường tròn (M).
Gọi I là trung điểm của OO', I là tâm của đường tròn có đường kính OO', IM là bán kính (vì MI là trung tuyến ứng với cạnh huyền của MOO'. IM là đường trung bình của hình thang OBCO' nên IM // OB // O'C. Do đó IM ⊥ BC.
BC vuông góc với IM tại M nên BC là tiếp tuyến của đường tròn (I).
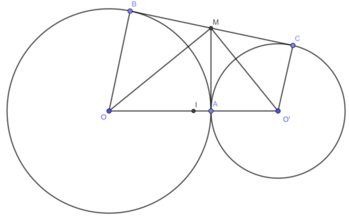
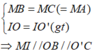
a) Ta thấy ngay AY chính là tiếp tuyến chung của hai đường tròn (O) và (O')
Theo tính chất hai tiếp tuyến cắt nhau, ta có YB = YA = YC
Vậy nên tam giác BAC vuông tại A hay \(\widehat{BAC}=90^o\)
b) Theo tính chất hai tiếp tuyến cắt nhau ta có \(\widehat{AYO}=\widehat{OYB};\widehat{AYO'}=\widehat{O'YC}\)
\(\Rightarrow\widehat{OYO'}=\widehat{OYA}+\widehat{AYO'}=90^o\)
Xét tam giác vuông OYO' có YK là trung tuyến ứng với cạnh huyền nên \(KY=\frac{OO'}{2}\)
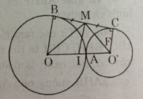
c) Ta thấy ngay BOO'C là hình thang vuông có Y là trung điểm BC, K là trung điểm OO' nên KY là đường trung bình của hình thang.
Vậy thì KY // OB // O'C
Từ đó ta có ngay KY vuông góc BC.
Lại có \(KY=KO\)
Nên BC là tiếp tuyến của đường tròn tâm K, bán kính KO.