cho tam giác ABC có AB=4,5cm AC=6cm BC=7cm.xác định dạng của tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng ĐL pi - ta - go đảo :
\(AB^2+BC^2=AC^2\)
\(< =>4.5^2+6^2=7.5^2\)
Do \(4.5^2+6^2=7.5^2\)đúng
=>ĐPCM

Áp dụng định lí Py-ta-go,ta có:
BC2=AC2+AB2
=4,52+62
=20,25+36
=56,25
mà\(\sqrt{56,25}\)=7,5
Suy ra tam giác ABC là tam giác vuông.

Ta có: 20,25+36=56,25
=>4,52+62=7,52
Hay AB2+BC2=AC2
=> Tam giác ABC vuông tại B

Ta có:
A B 2 = 6 2 = 36 A C 2 = 4 , 52 = 20 , 25 B C 2 = 7 , 52 = 56 , 25
Vì A B 2 + A C 2 = 36 + 20,25 = 56,25 = B C 2 nên tam giác ABC vuông tại A (theo định lí đảo Pi-ta-go)
Kẻ AH ⊥ BC
Ta có: AH.BC = AB.AC
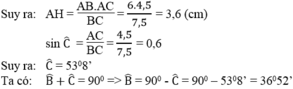
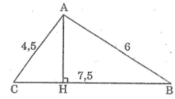

Ta có: AB2 + AC2 = 62 + 4,52 = 7,52 = BC2
nên tam giác ABC vuông tại A. (đpcm)
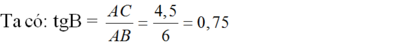
=> ∠B = 37o
=> ∠C = 90o - ∠B = 90o - 37o = 53o
Mặt khác trong tam giác ABC vuông tại A, ta có:
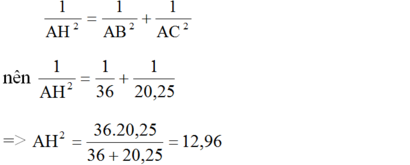
=> AH = 3,6 cm

TK
Diện tích tam giác là:
(4,5 x 6)/2=13,5 cm
Chiều cao AH là:
(13,5 x 2)/7,5=3,6 cm

Giải
Độ dài chiều cao AH là :
( 4,5 + 6 ) : 2 = 5,25 ( cm )
Đáp số : 5,25 cm
Mong bạn k mk
yến nhi libra virgo hotgirl sakura trả lời chính xác
quá đúng...!!
tk mk nha
thanks

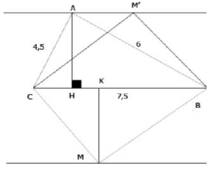
a) Ta có: \(\dfrac{AN}{AB}=\dfrac{3}{6}=\dfrac{1}{2}\)
\(\dfrac{AM}{AC}=\dfrac{4.5}{9}=\dfrac{1}{2}\)
Do đó: \(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)\(\left(=\dfrac{1}{2}\right)\)
Xét ΔANM và ΔABC có
\(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)(cmt)
\(\widehat{BAC}\) chung
Do đó: ΔANM\(\sim\)ΔABC(c-g-c)