cho hình chữ nhật ABCD gọi P,Q lll trung điểm của BC và AD gọi M là trung điểm của AP và BQ, N là giao điểm của CQ và DP chứng minh MPNQ là hình thoi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 11 2018
MỌI NGƯỜI GIÚP MÌNH TRONG HÔM NAY VỚI Ạ !!! MAI MÌNH KIỂM TRA RÙI !!! THANK KIU EVERYONE, MONG NHẬN ĐK CÂU TRẢ LỜI SỚM ( MÀ MỌI NGƯỜI KHÔNG CẦN VX HÌNH ĐÂU Ạ ^^)
TD
11 tháng 11 2018
1) a. xét trong tam giác ABC có
I trung điểm AB và K trung điểm AC =>IK là đường trung bình của tam giác ABC=>IK song song với BC
vậy BCKI là hình thang (vì có hai cạng đáy song song)
b.
IK // và =1/2BC (cm ở câu a) =>IK song song NM
M trung điểm HC và N trung điểm HB mà HB+HC=CB =>MN=IK=1/2BC
suy ra MKIN là hbh => có hai đường chéo bằng nhau =>IM=NK
18 tháng 1 2022
a: Xét tứ giác ABNM có
AM//BN
AM=BN
Do đó: ABNM là hình bình hành
mà \(\widehat{MAB}=90^0\)
nên ABNM là hình chữ nhật
mà AM=AB
nên ABNM là hình vuông
b: Xét ΔMBC có
MN là đường trung tuyến
MN=BC/2
Do đó: ΔMBC vuông tại M
Xét tứ giác MDCN có
MD//CN
MD=CN
Do đó: MDCN là hình bình hành
mà MD=DC
nên MDCN là hình vuông
Xét tứ giác MPNQ có
\(\widehat{MPN}=\widehat{MQN}=\widehat{PMQ}=90^0\)
Do đó: MPNQ là hình chữ nhật
20 tháng 11 2022
Xét tứ giác BPDQ có
BP//DQ
BP=DQ
Do đó: BPDQ là hình bình hành
=>BQ//DP
=>QM//NP
Xét tứ giác APCQ có
AQ//CP
AQ=CP
Do đó: APCQ là hình bình hành
=>PA//CQ
=>MP//QN
Xéttứ giác ABPQ có
AQ//BP
AQ=BP
góc BAQ=90 độ
Do đó: ABPQ là hình chữ nhật
=>AP cắt BQ tạit rung điểm của mỗi đường và AP=BQ
=>MQ=MP
Xét tứ giác MPNQ có
MP//NQ
MQ//NP
MQ=MP
Do đó: MPNQ là hình thoi
CM
25 tháng 3 2017
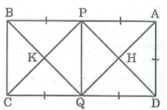
* Xét tứ giác APQD, ta có: AB // CD (gt) hay AP // QD
AP = 1/2 .AB (gt)
QD = 1/2 CD (gt)
AB= CD (vì ABCD là hình chữ nhật)
Suy ra: AP = QD
Hay tứ giác APQD là hình bình hành.
Lại có: ∠ A = 90 0 (vì tứ giác ABCD là hình chữ nhật)
Suy ra tứ giác APQD là hình chữ nhật.
Mà AD = AP = 1/2 AB
Vậy tứ giác APQD là hình vuông.
⇒ AQ ⊥ PD (t/chất hình vuông) ⇒ ∠ (PHQ) = 90 0 (1)
HP = HQ (t/chất hình vuông)
* Xét tứ giác PBCQ, ta có: AB // CD hay BP //CQ
PB = 1/2 AB (gt)
CQ = 1/2 CD (gt)
AB = CD do ABCD là hình chữ nhật
Suy ra: PB = CQ nên tứ giác PBCQ là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Lại có: ∠ B = 90 0 (vì ABCD là hình chữ nhật) suy ra tứ giác PBCQ là hình chữ nhật
PB = BC ( vì cùng bằng AD = 1/2 AB)
Vậy tứ giác PBCQ là hình vuông
⇒ PC ⊥ BQ (t/chất hình vuông) ⇒ ∠ (PKQ) = 90 0 (2)
PD là tia phân giác ∠ (APQ) ( t/chất hình vuông)
PC là tia phân giác ∠ (QPB) (t/chất hình vuông)
Suy ra: PD ⊥ PC (t/chất tia phân giác của hai góc kề bù) ⇒ ∠ (HPK) = 90 0 (3)
Từ (1), (2) và (3) suy ra tứ giác PHQK là hình vuông.
