Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

MỌI NGƯỜI GIÚP MÌNH TRONG HÔM NAY VỚI Ạ !!! MAI MÌNH KIỂM TRA RÙI !!! THANK KIU EVERYONE, MONG NHẬN ĐK CÂU TRẢ LỜI SỚM ( MÀ MỌI NGƯỜI KHÔNG CẦN VX HÌNH ĐÂU Ạ ^^)
1) a. xét trong tam giác ABC có
I trung điểm AB và K trung điểm AC =>IK là đường trung bình của tam giác ABC=>IK song song với BC
vậy BCKI là hình thang (vì có hai cạng đáy song song)
b.
IK // và =1/2BC (cm ở câu a) =>IK song song NM
M trung điểm HC và N trung điểm HB mà HB+HC=CB =>MN=IK=1/2BC
suy ra MKIN là hbh => có hai đường chéo bằng nhau =>IM=NK

a: Xét tứ giác ABNM có
AM//BN
AM=BN
Do đó: ABNM là hình bình hành
mà \(\widehat{MAB}=90^0\)
nên ABNM là hình chữ nhật
mà AM=AB
nên ABNM là hình vuông
b: Xét ΔMBC có
MN là đường trung tuyến
MN=BC/2
Do đó: ΔMBC vuông tại M
Xét tứ giác MDCN có
MD//CN
MD=CN
Do đó: MDCN là hình bình hành
mà MD=DC
nên MDCN là hình vuông
Xét tứ giác MPNQ có
\(\widehat{MPN}=\widehat{MQN}=\widehat{PMQ}=90^0\)
Do đó: MPNQ là hình chữ nhật

Xét tứ giác BPDQ có
BP//DQ
BP=DQ
Do đó: BPDQ là hình bình hành
=>BQ//DP
=>QM//NP
Xét tứ giác APCQ có
AQ//CP
AQ=CP
Do đó: APCQ là hình bình hành
=>PA//CQ
=>MP//QN
Xéttứ giác ABPQ có
AQ//BP
AQ=BP
góc BAQ=90 độ
Do đó: ABPQ là hình chữ nhật
=>AP cắt BQ tạit rung điểm của mỗi đường và AP=BQ
=>MQ=MP
Xét tứ giác MPNQ có
MP//NQ
MQ//NP
MQ=MP
Do đó: MPNQ là hình thoi

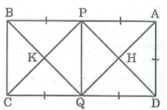
* Xét tứ giác APQD, ta có: AB // CD (gt) hay AP // QD
AP = 1/2 .AB (gt)
QD = 1/2 CD (gt)
AB= CD (vì ABCD là hình chữ nhật)
Suy ra: AP = QD
Hay tứ giác APQD là hình bình hành.
Lại có: ∠ A = 90 0 (vì tứ giác ABCD là hình chữ nhật)
Suy ra tứ giác APQD là hình chữ nhật.
Mà AD = AP = 1/2 AB
Vậy tứ giác APQD là hình vuông.
⇒ AQ ⊥ PD (t/chất hình vuông) ⇒ ∠ (PHQ) = 90 0 (1)
HP = HQ (t/chất hình vuông)
* Xét tứ giác PBCQ, ta có: AB // CD hay BP //CQ
PB = 1/2 AB (gt)
CQ = 1/2 CD (gt)
AB = CD do ABCD là hình chữ nhật
Suy ra: PB = CQ nên tứ giác PBCQ là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Lại có: ∠ B = 90 0 (vì ABCD là hình chữ nhật) suy ra tứ giác PBCQ là hình chữ nhật
PB = BC ( vì cùng bằng AD = 1/2 AB)
Vậy tứ giác PBCQ là hình vuông
⇒ PC ⊥ BQ (t/chất hình vuông) ⇒ ∠ (PKQ) = 90 0 (2)
PD là tia phân giác ∠ (APQ) ( t/chất hình vuông)
PC là tia phân giác ∠ (QPB) (t/chất hình vuông)
Suy ra: PD ⊥ PC (t/chất tia phân giác của hai góc kề bù) ⇒ ∠ (HPK) = 90 0 (3)
Từ (1), (2) và (3) suy ra tứ giác PHQK là hình vuông.