Cho a,b,c >0 và a+b+c = 1. Chứng minh b+c ≥ 16abc.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
2
T
27 tháng 11 2015
Áp dụng bđt coossi ta dduowcj : \(a+b+c\ge2\sqrt{a\left(b+c\right)}\Rightarrow1\ge4a\left(b+c\right)\Rightarrow b+c\ge4a\left(b+c\right)^2\)
Mà \(\left(b+c\right)^2\ge4bc\Rightarrow b+c\ge16abc\)
Dấu = xảy ra khi a=b+c và b=c và a+b+c=1=>a=1/2;b=c=1/4
0
2
4 tháng 4 2018
Áp dụng BĐT cô si cho 2 số không âm
\(b+c\ge2\sqrt{bc}\)
<=>\(\left(b+c\right)^2\ge4bc\) (1)
Áp dụng BĐT cô si cho 2 số không âm
\(a+\left(b+c\right)\ge2\sqrt{a\left(b+c\right)}\)
<=>\(\left[a+\left(b+c\right)\right]^2\ge4a\left(b+c\right)\)
<=>\(1\ge4a\left(b+c\right)\) (2)
nhân (1) với (2) ta đc
\(\left(b+c\right)^2\ge16abc.\left(b+c\right)\)
<=>\(b+c\ge16abc\) (đpcm)
30 tháng 6 2019
\(1=\left(a+b+c\right)^2\ge4a\left(b+c\right)\)
\(\Rightarrow b+c\ge4a\left(b+c\right)^2\ge4a\cdot4bc=16abc\)
Dấu "=" \(\Leftrightarrow\left\{{}\begin{matrix}a=b+c\\b=c\\a+b+c=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\frac{1}{2}\\b=c=\frac{1}{4}\end{matrix}\right.\)
HP
1 tháng 6 2016
Áp dụng bất đẳng thức Cô-Si (\(a+b\ge2\sqrt{ab}\)) ta được:
\(a+1\ge2\sqrt{a}\)
\(b+1\ge2\sqrt{b}\)
\(a+c\ge2\sqrt{ac}\)
\(b+c\ge2\sqrt{bc}\)
Nhân từng vế các BĐT trên :
=>\(\left(a+1\right)\left(b+1\right)\left(a+c\right)\left(b+c\right)\ge2\sqrt{a}.2\sqrt{b}.2\sqrt{ac}.2\sqrt{bc}=16abc\) (đpcm)
HC
0
XB
1
VT
1
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 4 2020
\(\left(a+b+c\right)^2\ge4a\left(b+c\right)\Rightarrow4a\left(b+c\right)\le1\)
\(\Rightarrow b+c\ge4a\left(b+c\right)^2\ge4a.4bc=16abc\)
\(\Rightarrow16abc-b-c\le0\)
\(\Rightarrow P_{max}=0\) khi \(\left(a;b;c\right)=\left(1;0;0\right);\left(\frac{1}{2};\frac{1}{4};\frac{1}{4}\right)\)
Ta có \(1=a+b+c\ge a+b\Rightarrow a\le1-b\)
\(Q=16ab-b-c\le16ab-b\le16\left(1-b\right)b-b\)
\(Q\le-16b^2+15b=\frac{225}{64}-16\left(b-\frac{15}{32}\right)^2\le\frac{225}{64}\)
\(Q_{max}=\frac{225}{64}\) khi \(\left(a;b;c\right)=\left(\frac{17}{32};\frac{15}{32};0\right)\)
DT
1
AH
Akai Haruma
Giáo viên
5 tháng 1 2019
Lời giải:
Áp dụng BĐT Cô-si dạng $(x+y)^2\geq 4xy$ và kết hợp với điều kiện $a+b+c=1$ ta có:
\(b+c=(b+c)(a+b+c)^2\geq (b+c).4a(b+c)=4a(b+c)^2\geq 4a.4bc=16abc\)
Ta có đpcm
Dấu "=" xảy ra khi \((a,b,c)=(\frac{1}{2}; \frac{1}{4}; \frac{1}{4})\), hoặc $(a,b,c)=(1,0,0)$
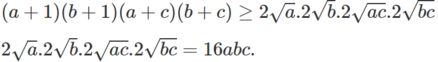
\(\left(b+c\right)\left(a+b+c\right)^2=\left(b+c\right)\left(a+\left(b+c\right)\right)^2\ge2\sqrt{bc}.4a\left(b+c\right)\)
\(\ge8\sqrt{bc}.a.2\sqrt{bc}\ge16abc\)
Dấu "=" xảy ra bạn tự kiếm nhé
u trả lời hay nhất: ta có (b+c)^2/4>=bc =>16abc=<16a(b+c)^2/4=4a(b+c) =4a (1-a)^2 =4a (1-a)(1-a) =(4a-4a^2)(1-a)
=(1-a) (1- (2a-1)^2)
Vì (2a-1)^2 >= 0 nên 1- (2a-1)^2 =< 1 suy ra (1-a) (1- (2a-1)^2) =<b+c
Vậy 16abc=< b+c
p/s :kham khảo