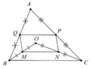
cho tam giác ABC gọi O là điểm thuộc miền trong của tam giác. M,N,P,Q thứ tự là trung điểm cua OP,OC,AC,AB
Chứng minh:a) MNPQ là hình bình hành
b) Xác định vị trí điểm O để tứ giác MNPQ là hình chữ nhật
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 9 2018
a) HS tự chứng minh
b) O nằm trên đường cao xuất phát từ đỉnh A của DABC
12 tháng 11 2021
o giả thiết cho IJ không song song với CDvà chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K=IJ∩CDK=IJ∩CD.
Ta có : M là điểm chung thứ nhất của (ACD) và (IJM);
{K∈IJIJ⊂(MIJ)⇒K∈(MIJ){K∈IJIJ⊂(MIJ)⇒K∈(MIJ) và {K∈CDCD⊂(ACD)⇒K∈(ACD){K∈CDCD⊂(ACD)⇒K∈(ACD)
Vậy (MIJ)∩(ACD)=MK(MIJ)∩(ACD)=MK
Quảng cáo
b) Với L=JN∩ABL=JN∩AB ta có:
{L∈JNJN⊂(MNJ)⇒L∈(MNJ){L∈JNJN⊂(MNJ)⇒L∈(MNJ)
{L∈ABAB⊂(ABC)⇒L∈(ABC){L∈ABAB⊂(ABC)⇒L∈(ABC)
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P=JL∩AD,Q=PM∩ACP=JL∩AD,Q=PM∩AC
Ta có:
{Q∈PMPM⊂(MNP)⇒Q∈(MNJ){Q∈PMPM⊂(MNP)⇒Q∈(MNJ)
Và {Q∈ACAC⊂(ABC)⇒Q∈(ABC){Q∈ACAC⊂(ABC)⇒Q∈(ABC)
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ=(ABC)∩(MNJ)LQ=(ABC)∩(MNJ).
25 tháng 9 2018
Bài khá dài đó.
Sorry nhé mik mới lớp 6 ak nên ko bít, tha lỗi nha!
ý kiến gì thì nhắn tin cho mik mai 7g
pp, ngủ ngon!
FG
15 tháng 10 2017
a) xét tam giác ABC, có:
E là trung điểm AB (gt)
F là trung điểm AC (gt)
=> EF là đtb (đường trung bình) tam giác ABC
=> EF // BC (1)
xét tam giác BMC, có:
K là trung điểm BM (gt)
I là trung điểm MC (gt)
=> KI là đtb tam giác BMC
=> KI // BC (2)
từ (1),(2):
=> EF // KI
ta có: EF là đtb (cmt)
=>EF = \(\frac{BC}{2}\)(3)
ta có: KI là đtb (cmt)
=> KI = \(\frac{BC}{2}\)(4)
từ (3),(4):
=> EF = KI
ta có: EF // KI (cmt)
EF = KI (cmt)
=> EFIK là hbh (tứ giác có 1 cặp cạnh đối vừa = nhau vừa //)
b) chưa biết làm :V
