Cho đa thức P(x)= x^4+x^3+6x^2-40x+m=1979.
a, Tìm m sao cho P(x) chia hết cho x-2
b, Với m vừa tìm được, giải phương trình P(x)=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: P(x) chia hết cho x-2
=>x^4-2x^3+3x^3-6x^2+12x^2-24x-16x+32+m-2017 chia hết cho x-2
=>m-2017=0
=>m=2017
b: P(x)=x^4+x^3+6x^2-40x+32
P(x)=0
=>x^4-2x^3+3x^3-6x^2+12x^2-24x-16x+32=0
=>(x-2)(x^3+3x^2+12x-16)=0
=>x^3+3x^2+12x-16=0 hoặc x-2=0
=>x^3-x^2+4x^2-4x+16x-16=0 hoặc x-2=0
=>x-1=0 hoặc x=2
=>x=1 hoặc x=2

p(x)=x^4-16+x^3 +8+6(x^2-4)-40(x+2)+m-2017+(16-8+24+80)
để p(x) chia hết cho x+2
m-2017+110=0
m=1907

\(x^4-x^3+6x^2-x+a=x^2\left(x^2-x+5\right)+x^2-x+a\)
Vậy a = 5

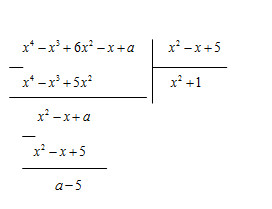
Vậy a = 5 thì đa thức x^4 - x^3 + 6x^2 - x +a chia hết cho đa thức x^2 - x + 5

1. Tổng các hệ số của đa thức là: 12004.22005=22005
2.Cần chứng minh x4+x3+x2+x+1=0 vô nghiệm.
Nhận thấy x = 1 không là nghiệm của phương trình .
Nhân cả hai vế của pt cho (x−1)≠0 được :
(x−1)(x4+x3+x2+x+1)=0⇔x5−1=0⇔x=1(vô lí)
Vậy pt trên vô nghiệm.
1. Tổng các hệ số của đa thức là:
12014 . 22015 = 22015
2 . Cần chứng minh.
\(x4 + x3 + x2 + x + 1 = 0\)
Vô nghiệm.
Ta nhận thấy \(x + 1 \) không là nghiệm của phương trình.
Nhân cả hai vế của phương trình cho:
\(( x - 1 ) \) \(\ne\) \(0\) được :
\(( x-1). (x4+x3+x2+x+1)=0\)
\(\Leftrightarrow\)\(5x-1=0\) \(\Leftrightarrow\) \(x = 1\)
Vô lí.
Vậy phương trình trên vô nghiệm.

Cau a va b dat cot tim so du .Vi la phep chia het nen du bang 0.Cau c thi da thuc se chia het cho tich (x+3)(x-3) lam tuong tu hai cau a va b
câu này giải sao bạn