Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: P(x) chia hết cho x-2
=>x^4-2x^3+3x^3-6x^2+12x^2-24x-16x+32+m-2017 chia hết cho x-2
=>m-2017=0
=>m=2017
b: P(x)=x^4+x^3+6x^2-40x+32
P(x)=0
=>x^4-2x^3+3x^3-6x^2+12x^2-24x-16x+32=0
=>(x-2)(x^3+3x^2+12x-16)=0
=>x^3+3x^2+12x-16=0 hoặc x-2=0
=>x^3-x^2+4x^2-4x+16x-16=0 hoặc x-2=0
=>x-1=0 hoặc x=2
=>x=1 hoặc x=2

p(x)=x^4-16+x^3 +8+6(x^2-4)-40(x+2)+m-2017+(16-8+24+80)
để p(x) chia hết cho x+2
m-2017+110=0
m=1907

\(x^4-x^3+6x^2-x+a=x^2\left(x^2-x+5\right)+x^2-x+a\)
Vậy a = 5

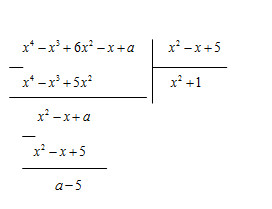
Vậy a = 5 thì đa thức x^4 - x^3 + 6x^2 - x +a chia hết cho đa thức x^2 - x + 5

Cau a va b dat cot tim so du .Vi la phep chia het nen du bang 0.Cau c thi da thuc se chia het cho tich (x+3)(x-3) lam tuong tu hai cau a va b

\(x^4-x^3+6x^2-x+a=\left(x^2+1\right)\left(x^2-x+5\right)+a-5\)
Để đa thức \(x^4-x^3+6x^2-x+a\) chia hết cho đa thức \(x^2-x+5\)
\(\Rightarrow a-5=0\Leftrightarrow a=5\)
b, Đặt \(2x^3-3x^2+x+a=f\left(x\right)\) và \(x+2=g\left(x\right)\)
Theo dịnh lí Bơ du ta có
Xét \(g\left(x\right)=0\Rightarrow x+2=0\Rightarrow x=-2\)
Để \(f\left(x\right)\) chia hết cho \(g\left(x\right)\) thì \(f\left(-2\right)=0\)
\(f\left(-2\right)=2.\left(-2\right)^3-3.\left(-2\right)^2-2+a=0\)
\(\Rightarrow f\left(x\right)=-16-12-2+a=0\)
\(\Rightarrow f\left(x\right)=-30+a=0\)
\(\Rightarrow a=30\)
Vậy \(a=30\) thì \(f\left(x\right)\) chia hết cho \(g\left(x\right)\)
Câu b) Thay x=-2 vào rồi giải theo phương pháp giá trị riêng
câu này giải sao bạn