Cho tam giác ABC có:AB<AC.Các điểm D,E lần lượt dịch chuyển trên ABvà tia đối CA sao cho BD=CE.CM các đường trung trực của DE luôn đi qua một điểm cố định
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông
và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
Cho tam giác ABC và tam giác DEF có: AB=DE,BC=EF,AC=DF.
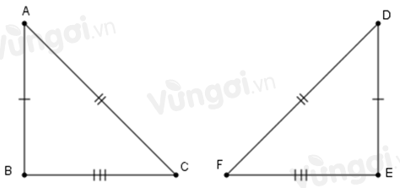
Xét ΔABC và ΔDEF có:
AB=DE(gt)
BC=EF(gt)
AC=DF(gt)
⇒ΔABC=ΔDEF (c.c.c).
Học tốt nhé!

a: Xét ΔABC và ΔADE có
AB/AD=AC/AE
góc A chung
=>ΔABC đồng dạng với ΔADE
b: ΔBAC đồng dạng với ΔDAE
=>góc ABC=góc ADE
=>BC//DE
c: AE+EC=AC
=>EC=8cm
BE là phân giác góc ABC
=>AB/AE=BC/CE
=>BC/8=9/4
=>BC=18cm
d: DE//BC
=>DE/BC=AE/AC=1/3
=>DE/18=1/3
=>DE=6cm

 Hình bạn chịu khó vào Thống kê hỏi đáp của mình xem
Hình bạn chịu khó vào Thống kê hỏi đáp của mình xem
Xét \(\Delta ABD\)và \(\Delta ADC\)có
\(AB\ne AD\)( 6cm < 8cm )
=> \(\Delta ABD< \Delta ADC\)( do AB < AD )
=> đpcm
* Lần đầu làm dạng này ... Có sai sót gì mong bạn bỏ qua *

- PABC=AB+AC+BC=5+7+9=21cm.
- Vì △ABC∼△MNP nên:
\(\dfrac{AB}{MN}=\dfrac{AC}{MP}=\dfrac{BC}{NP}=\dfrac{P_{ABC}}{P_{MNP}}=\dfrac{21}{5,25}=4\)
=>\(\left[{}\begin{matrix}MN=\dfrac{AB}{4}=\dfrac{5}{4}=1,25\left(cm\right)\\MP=\dfrac{AC}{4}=\dfrac{7}{4}=1,75\left(cm\right)\\NP=\dfrac{BC}{4}=\dfrac{9}{4}=2,25\left(cm\right)\end{matrix}\right.\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{MN}{5}=\dfrac{NP}{9}=\dfrac{MP}{7}=\dfrac{MN+NP+MP}{5+9+7}=\dfrac{5.25}{21}=0.25\)
Do đó: MN=1,25(cm); NP=2,25(cm); MP=1,75(cm)

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM
câu a có bạn bên trên là rồi nên mình sẽ làm câu b nha bạn ^^
b) Vì tam giác ABC cân có MA phân giác => MA vuông BC và M trung điểm BC. Vì MA = MD nên M trung điểm AD.
Xét tứ giác ABDC có M trung điểm AD và BC => hình bình hành
=> AB = CD, AB // CD

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM
Giúp mình với mai phải nộp rồi