Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- PABC=AB+AC+BC=5+7+9=21cm.
- Vì △ABC∼△MNP nên:
\(\dfrac{AB}{MN}=\dfrac{AC}{MP}=\dfrac{BC}{NP}=\dfrac{P_{ABC}}{P_{MNP}}=\dfrac{21}{5,25}=4\)
=>\(\left[{}\begin{matrix}MN=\dfrac{AB}{4}=\dfrac{5}{4}=1,25\left(cm\right)\\MP=\dfrac{AC}{4}=\dfrac{7}{4}=1,75\left(cm\right)\\NP=\dfrac{BC}{4}=\dfrac{9}{4}=2,25\left(cm\right)\end{matrix}\right.\)

![]()
Suy ra: tam giác ABC vuông tại A.
Diện tích tam giác ABC là:
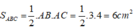
*Gọi tam giác ABC đồng dạng với tam giác MNP theo tỉ số k
Suy ra:
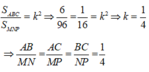
Thay số
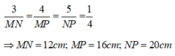
Chọn đáp án B

AB/MN=BC/NP=CA/PM=(AB+BC+CA)/(MN+NP+PM)=(2+3+4)/36=1/4
=> AB/MN=2/MN=1/4=> MN=8
Tương tự tính ra NP và PM
Tính chu vi của tam giác ABC là:9cm
Lấy chu vi tam giác MNP/tam giác ABC là: 36/9=4cm
=>MN=4.2=8(cm)
NP=4.3=12(cm)
MP=4.4=16(cm)

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
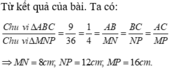
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{MN}{5}=\dfrac{NP}{9}=\dfrac{MP}{7}=\dfrac{MN+NP+MP}{5+9+7}=\dfrac{5.25}{21}=0.25\)
Do đó: MN=1,25(cm); NP=2,25(cm); MP=1,75(cm)