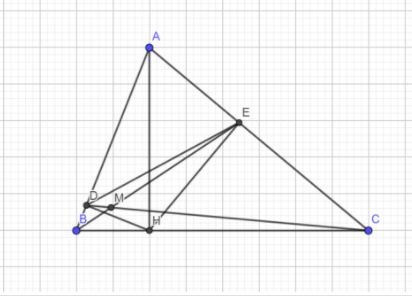
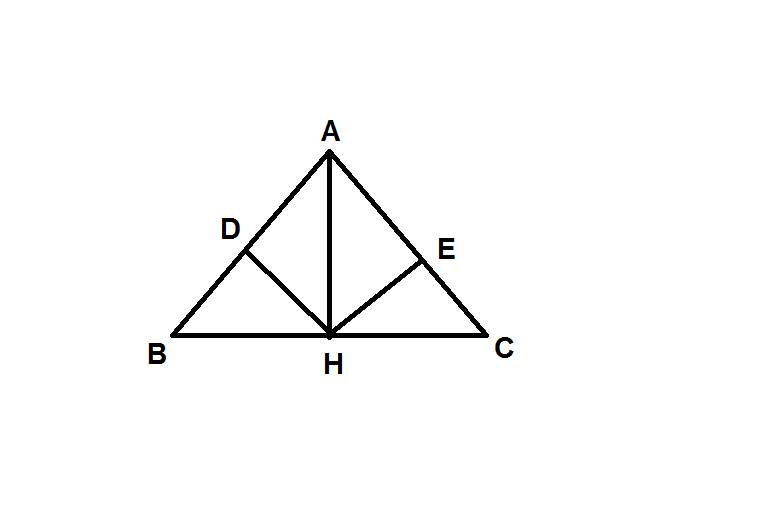
Cho tam giác ABC có AH là đường cao ( H thuộc BC). Gọi E và D lần lượt là hình chiếu
của H trên AB và AC. Chứng minh rằng :
a)tam giác ABH ~ tam giác AHE
b) HE2 = AE. BE
c) Gọi M là giao điểm của BD và CE. Chứng minh rằng tam giác ADE ~ tam giác ABC.
d) Chứng minh góc HAD = góc DEH



a) Xét ΔABH vuông tại H và ΔAHE vuông tại E có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔAHE(g-g)
b) Xét ΔAEH vuông tại E và ΔHEB vuông tại E có
\(\widehat{EAH}=\widehat{EHB}\left(=90^0-\widehat{EBH}\right)\)
Do đó: ΔAEH\(\sim\)ΔHEB(g-g)
Suy ra: \(\dfrac{EA}{EH}=\dfrac{EH}{EB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(HE^2=AE\cdot BE\)(đpcm)