Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. Xét tam giác $ABH$ và $AHD$ có:
$\widehat{A}$ chung
$\widehat{AHB}=\widehat{ADH}=90^0$
$\Rightarrow \triangle ABH\sim \triangle AHD$ (g.g)
b. Xét tam giác $AEH$ và $HEC$ có:
$\widehat{AEH}=\widehat{HEC}=90^0$
$\widehat{EAH}=90^0-\widehat{AHE}=\widehat{EHC}$
$\Rightarrow \triangle AEH\sim \triangle HEC$ (g.g)
$\Rightarrow \frac{AE}{EH}=\frac{HE}{EC}$
$\Rightarrow HE^2=AE.EC$
c. Từ $\triangle ABH\sim \triangle AHD$ (phần a) suy ra:
$\frac{AB}{AH}=\frac{AH}{AD}$
$\Rightarrow AH^2=AB.AD$
Tương tự ta cũng có thể cm $\triangle AHE\sim \triangle ACH$
$\Rightarrow AH^2=AE.AC$
$\Rightarrow AB.AD=AE.AC$
$\Rightarrow \frac{AB}{AE}=\frac{AC}{AD}$
$\Rightarrow \triangle ABE\sim \triangle ACD$ (c.g.c)
$\Rightarrow \widehat{ABE}=\widehat{ACD}$ hay $\widehat{DBM}=\widehat{ECM}$
Xét tam giác $DBM$ và $ECM$ có:
$\widehat{DBM}=\widehat{ECM}$ (cmt)
$\widehat{DMB}=\widehat{EMC}$ (đối đỉnh)
$\Rightarrow \triangle DBM\sim \triangle ECM$ (g.g)

a: góc AEH=góc ADH=góc DAE=90 độ
=>ADHE là hình chữ nhật
b: Xét ΔABH vuông tại H và ΔAHD vuông tại D có
góc BAH chung
=>ΔABH đồng dạngvói ΔAHD
c: ΔHAC vuông tại H có HE là đường cao
nên HE^2=AE*EC

a, Xét △ABH và △AHD có:
∠AHB=∠ADH (=90o) , ∠BAH chung
⇒ △ABH ∼ △AHD (g.g)
b, Xét △AHE và △HCE có:
∠AHE=∠ACH (cùng phụ ∠AHC), ∠AEH=∠CEH (=90o)
⇒ △AHE ∼ △HCE (g.g)
⇒ \(\dfrac{HE}{EC}=\dfrac{AE}{HE}\) ⇒ HE2=AE.EC

a: Xét ΔABH vuông tại H và ΔAHD vuông tại D có
góc BAH chung
=>ΔABH đồng dạng với ΔAHD
b: ΔHAC vuông tại H có HE vuông góc AC
nên HE^2=AE*EC

Tam giác vuông ADH và tam giác vuông AHB có góc A chung nên đồng dạng => AD/AH = AH/AB => AH2 = AD.AB
cmtt ta cũng có AH2 = AE.AB => AD.AB = AE. AC
Xét tam giác ABE và tam giác ACD có góc A chung và AB/AC = AE/AD (cmt)
=> tg ABE đồng dạng tg ACD (c-g-c) => góc ABE = góc ACD
đến đây bn tự cm tiếp nhé!

a) Xét ΔABH vuông tại H và ΔAHE vuông tại E có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔAHE(g-g)
b) Xét ΔAEH vuông tại E và ΔHEB vuông tại E có
\(\widehat{EAH}=\widehat{EHB}\left(=90^0-\widehat{EBH}\right)\)
Do đó: ΔAEH\(\sim\)ΔHEB(g-g)
Suy ra: \(\dfrac{EA}{EH}=\dfrac{EH}{EB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(HE^2=AE\cdot BE\)(đpcm)
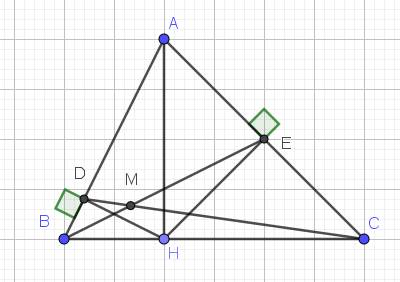



a: Xét ΔABH vuông tại H và ΔAHD vuông tại D có
góc BAH chung
Do đó: ΔABH∼ΔAHD
b: Xét ΔAHC vuông tại H có HE là đường cao
nên \(HE^2=AE\cdot EC\)