Gọi AM ,BN,CL là ba đường cao của tam giác ABC . Chứng minh :
- \(\Delta ANL\)~ \(\Delta ABC\)
- \(\frac{AN.BL.CM}{AB.BC.CA}\)=\(\cos A\).\(\cos B\).\(\cos C\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 7 2019
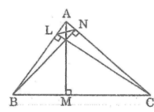
ABN vuông tại N nên AN = AB.cosB (1)
∆ BCL vuông tại L nên BL = BC.cosB (2)
∆ ACM vuông tại M nên CM = AC.cosC (3)
Từ (1), (2) và (3) suy ra: AN.BL.CM = AB.BC.CA. cosA cosB cosC
CM
12 tháng 10 2018
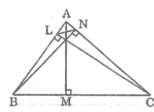
a. Xét hai tam giác BNA và CLA, ta có:
∠ BNA = ∠ CLA = 90 °
góc A chung
Suy ra ∆ BNA đồng dạng ∆ CLA (g.g)
Suy ra: AL/AN = AC/AB ⇒ AL/AC = AN/AB
Xét hai tam giác ABC và ANL, ta có:
AL/AC = AN/AB
góc A chung
Suy ra ∆ ABC đồng dạng ∆ ANL (c.g.c)
1, 2 tam giac vuong ANB va tam giac ALC co goc A chung nen 2 tam giac nay dong dang
\(\Rightarrow\frac{AN}{AB}=\frac{AL}{AC}\)
vi vay \(\Delta ANL~\Delta ABC\)
2, ta co \(AN=\cos A\cdot AB\) \(BL=\cos\cdot BC\) \(CM=\cos C\cdot AC\)
\(\Rightarrow AN\cdot BL\cdot CM=\cos A\cdot\cos B\cdot\cos C\cdot AB\cdot AC\cdot BC\)
hay\(\frac{AN\cdot BL\cdot CM}{AB\cdot BC\cdot CA}=\cos A\cdot\cos B\cdot\cos C\)