K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
20 tháng 7 2019
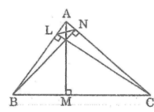
ABN vuông tại N nên AN = AB.cosB (1)
∆ BCL vuông tại L nên BL = BC.cosB (2)
∆ ACM vuông tại M nên CM = AC.cosC (3)
Từ (1), (2) và (3) suy ra: AN.BL.CM = AB.BC.CA. cosA cosB cosC

CM
12 tháng 10 2018
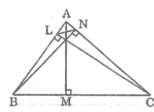
a. Xét hai tam giác BNA và CLA, ta có:
∠ BNA = ∠ CLA = 90 °
góc A chung
Suy ra ∆ BNA đồng dạng ∆ CLA (g.g)
Suy ra: AL/AN = AC/AB ⇒ AL/AC = AN/AB
Xét hai tam giác ABC và ANL, ta có:
AL/AC = AN/AB
góc A chung
Suy ra ∆ ABC đồng dạng ∆ ANL (c.g.c)
1, 2 tam giac vuong ANB va tam giac ALC co goc A chung nen 2 tam giac nay dong dang
\(\Rightarrow\frac{AN}{AB}=\frac{AL}{AC}\)
vi vay \(\Delta ANL~\Delta ABC\)
2, ta co \(AN=\cos A\cdot AB\) \(BL=\cos\cdot BC\) \(CM=\cos C\cdot AC\)
\(\Rightarrow AN\cdot BL\cdot CM=\cos A\cdot\cos B\cdot\cos C\cdot AB\cdot AC\cdot BC\)
hay\(\frac{AN\cdot BL\cdot CM}{AB\cdot BC\cdot CA}=\cos A\cdot\cos B\cdot\cos C\)