Mọi người chỉ mình câu 3b vs 4 với cảm ơn mn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
3 tháng 3 2023
em ơi chưa có bài em nhé, em chưa tải bài lên lám sao mình giúp được
28 tháng 8 2021
Bài 3:
b: Ta có: \(\sqrt{x^2-2x+1}=\left|x-2\right|\)
\(\Leftrightarrow\left|x-1\right|=\left|x-2\right|\)
\(\Leftrightarrow x-1=2-x\)
\(\Leftrightarrow2x=3\)
hay \(x=\dfrac{3}{2}\)
HN
28 tháng 8 2021
Bài 4: ĐK: x>0
a) \(B=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}+1-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\)
\(\Leftrightarrow B=\dfrac{\sqrt{x}\left[\left(\sqrt{x}\right)^3+1\right]}{x-\sqrt{x}+1}+1-\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}\)
\(\Leftrightarrow B=\dfrac{\sqrt{x}.\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1-2\sqrt{x}-1\)
\(\Leftrightarrow B=\sqrt{x}.\left(\sqrt{x}+1\right)-2\sqrt{x}=x+\sqrt{x}-2\sqrt{x}\)
\(\Leftrightarrow B=x-\sqrt{x}\)
Vậy với x>0 thì \(B=x-\sqrt{x}\)
b) Ta có: \(B=2\)
\(\Leftrightarrow x-\sqrt{x}=2\)
\(\Leftrightarrow x-\sqrt{x}-2=0\)
\(\Leftrightarrow x-2\sqrt{x}+\sqrt{x}-2=0\)
\(\Leftrightarrow\sqrt{x}.\left(\sqrt{x}-2\right)+\left(\sqrt{x}-2\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)=0\)
Do \(\sqrt{x}+1>0\) nên, ta suy ra:
\(\sqrt{x}-2=0\Leftrightarrow\sqrt{x}=2\Leftrightarrow x=4\) \(\left(TMĐK\right)\)
Vậy \(x=4\) thì \(B=2\)
H
5 tháng 4 2021
Để làm dạng này , bạn làm như sau :
Vì bạn biết 1 giờ = 60 phút; 1 phút =60 giây nên là
Trước hết bạn lấy số 0,8325 (số chỉ giờ) nhân 60 nhé = 49,95
Bạn lấy phần nguyên của nó trước dấu phẩy là 49 , điền vảo chỗ chấm trước phút.
Cái phần thập phân sau dấu phẩy là 0,95 bạn tiếp tục nhân 60 = 57.
Bạn điền 57 vào phần chỗ chấm trước giây.
Vậy 0,8325 giờ=49 phút 57 giây
LB
1
25 tháng 8 2021
Câu 3:
2: Xét tứ giác OKEH có
\(\widehat{OKE}=\widehat{OHE}=\widehat{KOH}=90^0\)
Do đó: OKEH là hình chữ nhật
mà đường chéo OE là tia phân giác của \(\widehat{KOH}\)
nên OKEH là hình vuông
LB
1
13 tháng 8 2021
18.\(\)\(=>I1=\dfrac{U}{R1}=\dfrac{16}{4R2}=\dfrac{4}{R2}A,\)
\(=>I2=\dfrac{U}{R2}=\dfrac{16}{R2}\left(A\right)\)
\(=>I2=I1+6< =>\dfrac{16}{R2}=\dfrac{4}{R2}+6< =>R2=2\left(ôm\right)\)
\(=>I1=\dfrac{4}{2}=2A,=>I2=2+6=8A\)
\(=>R1=4R2=8\left(ôm\right)\)
19
\(I2=1,5I1< =>\dfrac{U}{R2}=\dfrac{1,5U}{R1}=>\dfrac{1}{R2}=\dfrac{1,5}{R1}\)
\(< =>\dfrac{1}{R2}=\dfrac{1,5}{R2+5}=>R2=10\left(ôm\right)=>R1=R2+5=15\left(ôm\right)\)
PL
1
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 12 2021
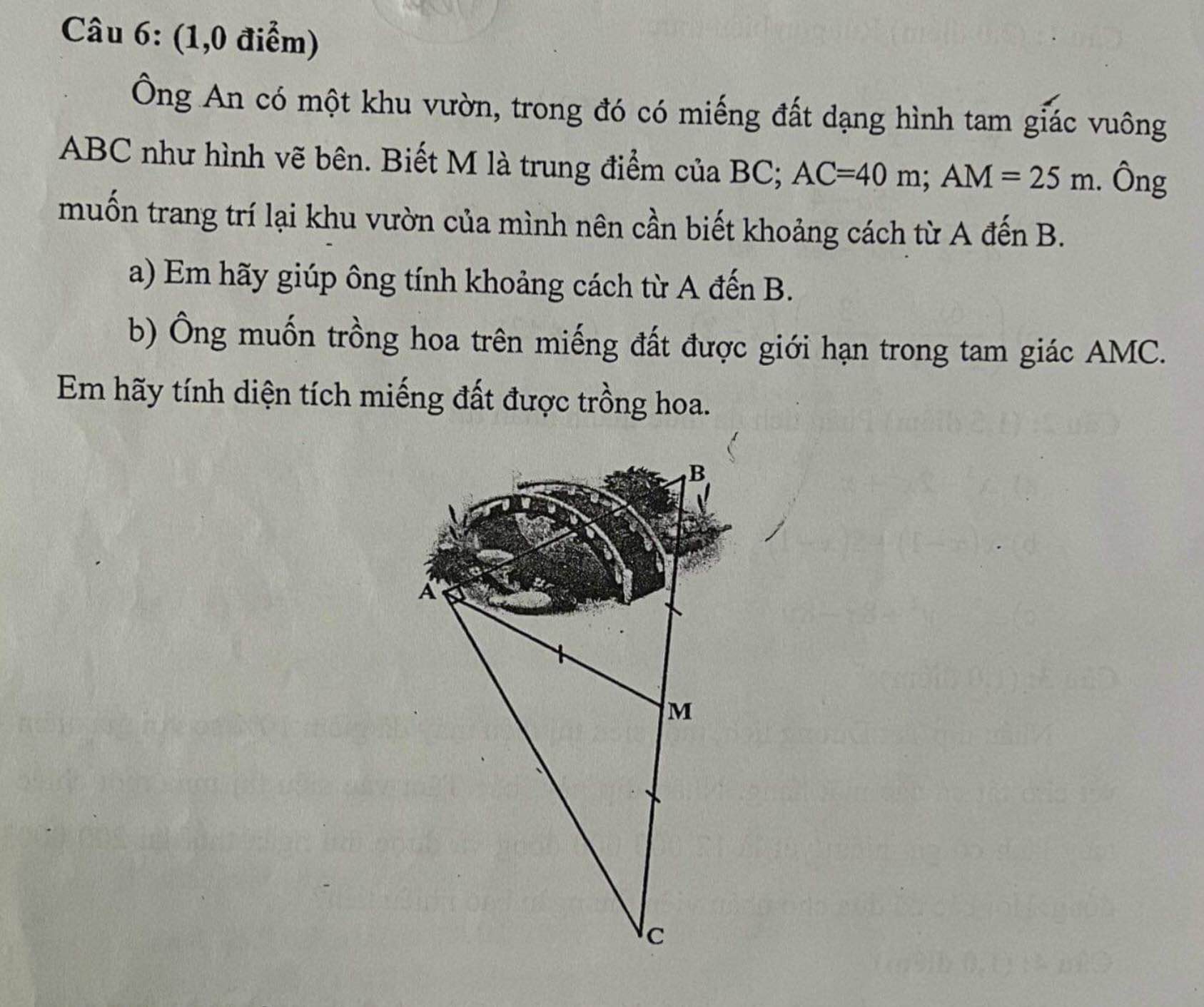
Tam giác ABC vuông tại A có AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC=2AM=50\left(m\right)\)
a. Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=30\left(m\right)\)
b. Kẻ \(MH\perp AC\Rightarrow MH||AB\) (cùng vuông góc AC)
Mà M là trung điểm BC \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH=\dfrac{1}{2}AB=15\left(m\right)\)
\(\Rightarrow S_{AMC}=\dfrac{1}{2}MH.AC=\dfrac{1}{2}.15.40=300\left(m^2\right)\)
Bài 3:
a) Xét ΔADB và ΔEDC có
\(\widehat{ADB}=\widehat{EDC}\)(hai góc đối đỉnh)
\(\widehat{BAD}=\widehat{CED}\)(hai góc so le trong, AB//CE)
Do đó: ΔADB\(\sim\)ΔEDC(g-g)
Bài 3:
b) Ta có: \(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
mà \(\widehat{BAD}=\widehat{CED}\)(hai góc so le trong, AB//CE)
nên \(\widehat{CAD}=\widehat{CED}\)
hay \(\widehat{CAE}=\widehat{CEA}\)
Xét ΔACE có \(\widehat{CAE}=\widehat{CEA}\)(cmt)
nên ΔCAE cân tại C(Định lí đảo của tam giác cân)
Suy ra: CA=CE(hai cạnh bên)
mà CA=20cm(gt)
nên CE=20cm
Ta có: ΔADB\(\sim\)ΔEDC(cmt)
nên \(\dfrac{AD}{DE}=\dfrac{AB}{EC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AD}{DE}=\dfrac{15}{20}=\dfrac{3}{4}\)