Chỉ cho em cách làm bài 28 với mái em thi rồi 😭
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 9 2021
\(a,\left\{{}\begin{matrix}Az\perp Ox\\Ox\perp Oy\left(\widehat{xOy}=90^0\right)\end{matrix}\right.\Rightarrow Az//Oy\)
\(b,\widehat{xOm}=\dfrac{1}{2}\widehat{xOy}=\dfrac{1}{2}\cdot90^0=45^0\left(t/c.phân.giác\right)\\ \widehat{nAx}=\dfrac{1}{2}\widehat{xAz}=\dfrac{1}{2}\cdot90^0=45^0\left(t/c.phân.giác\right)\\ \Rightarrow\widehat{xOm}=\widehat{nAx}\left(=45^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(Om//An\)
DT
2
L
19 tháng 5 2022
cẩn thận là được bạn ạ, có thể luyện tập dần đi cũng được, vẽ mấy hình trong sgk, sbt hay trên mạng cũng có á
TT
2
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
\(\left(3x+1\right)^2=9x^2+6x+1\)
\(\left(-4+x\right)^2=16-8x+x^2\)
\(9+12x+4x^2=\left(3+2x\right)^2\)
d giống a, e giống b (đề bị lặp)
18 tháng 8 2021
a: \(\left(3x+1\right)^2=9x^2+6x+1\)
b: \(\left(-4+x\right)^2=16-8x+x^2\)
c: \(9+12x+4x^2=\left(3+2x\right)^2\)
d: \(\left(3x+1\right)^2=9x^2+6x+1\)
e: \(\left(-4+x\right)^2=16-8x+x^2\)
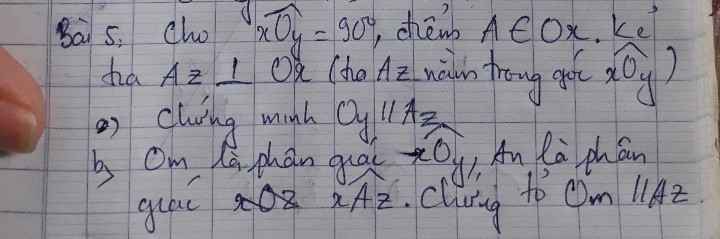
Do Δ là phương trình đường thẳng ⇒ m ≠ 0
Đến đây có thể chọn D được luôn. Và đây là cách làm chi tiết
Nếu m = 2 thì phương trình của d và delta lần lượt là .... và .... Tìm tọa độ của hệ sẽ thấy nó có 1 cặp nghiệm x,y => m = 2 thì d và delta cắt nhau, không thỏa mãn
Nếu m khác 2
Để Δ // d
⇒ \(\left\{{}\begin{matrix}\dfrac{m+3}{m}=\dfrac{2}{m}\\\dfrac{2}{m}\ne\dfrac{-6}{2-m}\end{matrix}\right.\) Giải ra
Với \(m=0\) thi \(\Delta\) trở thành: \(2=0\) (vô lý)
\(\Rightarrow\) Loại trường hợp \(m=0\) đồng nghĩa loại 3 đáp án A; B; C
Do đó D đúng