Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a=\dfrac{1}{9}.\left(999...9\right)=\dfrac{1}{9}.\left(100...0-1\right)=\dfrac{1}{9}\left(10^n-1\right)\)
\(b=100...0+5=10^n+5\)
\(\Rightarrow ab+1=\dfrac{1}{9}\left(10^n-1\right)\left(10^n+5\right)+1=\dfrac{1}{9}\left(10^{2n}+4.10^n+4\right)=\dfrac{1}{9}\left(10^n+2\right)^2\)
\(=\left(\dfrac{10^n+2}{3}\right)^2\)
Ta có: \(10\equiv1\left(mod3\right)\Rightarrow10^n\equiv1\left(mod3\right)\)
\(\Rightarrow10^n+2⋮3\)
\(\Rightarrow\dfrac{10^n+2}{3}\in Z\)
\(\Rightarrow\left(\dfrac{10^n+2}{3}\right)^2\) là SCP hay \(ab+1\) là SCP

a.
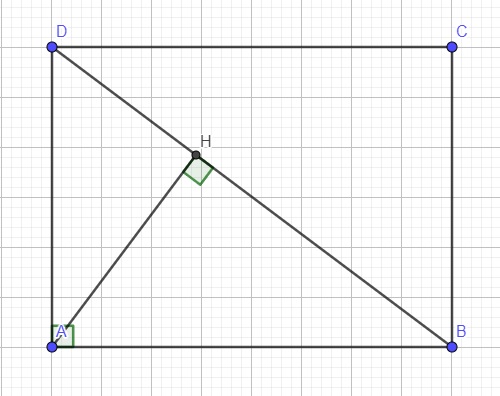
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)

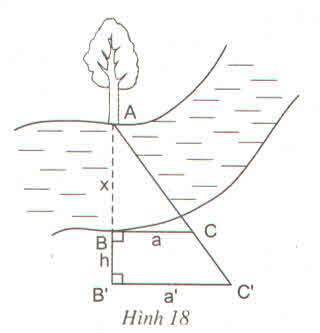
Ta có:
= mà AB' = x + h nên
= <=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng
cẩn thận là được bạn ạ, có thể luyện tập dần đi cũng được, vẽ mấy hình trong sgk, sbt hay trên mạng cũng có á
Anh chỉ cần vẽ đúng theo yêu cầu là được rồi