cô vừ giao cho mình câu sau
Bạn An chọn ngẫu nhiêu 3 quả trong 1 hộp gồm 19 quả đánh số từ 1 đến 19 tỉnh sác suất để bạn An chọn ra 3 quả có tổng chia hết cho 4Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(n\left(\Omega\right)=C^3_{30}=4060\)
n(A)\(C^1_{15}\cdot C^2_{15}=1575\)
=>P=1575/4060=45/116

Chia 16 số ra làm 3 tập:
A={1;4;7;10;13;16}; B={2;5;8;11;14}; C={3;6;9;12;15}
TH1: 1 số trong A, 1 số trong B, 1 số trong C
=>Có 6*5*5=150 cách
TH2: 3 số trong A
=>Có \(C^3_6=20\left(cách\right)\)
TH3: 3 số trong B hoặc C
=>Có \(C^3_5\cdot2=20\left(cách\right)\)
=>n(A)=20+20+150=190
\(n\left(omega\right)=C^3_{16}=560\)
=>P(A)=19/56

Không gian mẫu: \(C_{15}^3=455\)
Số cách chọn 3 quả sao cho vừa khác màu vừa khác số:
\(4.4.4=64\)
Xác suất: \(P=\dfrac{64}{455}\)

Đáp án C
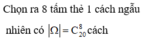
Trong 20 tấm thẻ có 10 tấm mang
số lẻ, có 5 tấm mang số chẵn không chia hết cho 4 và 5 tấm thẻ mang số chẵn
chia hết cho 4
TH1: Lấy được 5 tấm mang số lẻ, 2 tấm mang số chẵn chia hết cho 4 và tấm mang 1 số chẵn không chi hết cho 4 có ![]()
TH2: Lấy được 5 tấm mang số lẻ, 3 tấm mang số chẵn chia hết cho 4 có
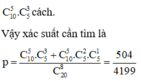

Đáp án C
Chọn ra 8 tấm thẻ 1 cách ngẫu nhiên có ![]() cách
cách
Trong 20 tấm thẻ có 10 tấm mang số lẻ, có 5 tấm mang số chẵn không chia hết cho 4 và 5 tấm thẻ mang số chẵn chia hết cho 4
TH1: Lấy được 5 tấm mang số lẻ, 2 tấm mang số chẵn chia hết cho 4 và tấm mang 1 số chẵn không chi hết cho 4 có: ![]()
TH2: Lấy được 5 tấm mang số lẻ, 3 tấm mang số chẵn chia hết cho 4 có ![]() cách.
cách.
Vậy xác suất cần tìm là
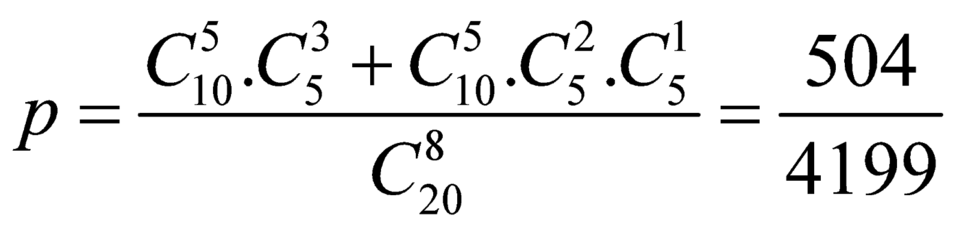

Không gian mẫu là số cách chọn ngẫu nhiên 3 viên bi từ hộp chứa 50 viên bi.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố “3 viên bi được chọn là một số chia hết cho 3 ’’.
Trong 50 viên bi được chia thành ba loại gồm: 16 viên bi có số chia hết cho 3; 17 viên bi có số chia cho 3 dư 1 và 17 viên bi còn lại có số chia cho 3 dư 2.
Để tìm số kết quả thuận lợi cho biến cố A, ta xét các trường hợp
● Trường hợp 1. 3 viên bi được chọn cùng một loại, có ![]() cách.
cách.
● Trường hợp 2. 3 viên bi được chọn có mỗi viên mỗi loại, có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]() .
.
Vậy xác suất cần tính 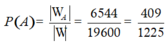
Chọn B.
Số phần tử của không gian mẫu \(\left|\Omega\right|=C^3_{19}\)
Gọi A là biến cố: "An chọn ra 3 quả cho tổng chia hết cho 4."
Trong các số từ 1 đến 19 sẽ có 4 số chia hết cho 4; 5 số chia 4 dư 1; 5 số chia 4 dư 2 và 5 số chia 4 dư 3. Để tổng các số trên 3 quả chia hết cho 4 thì số dư của bộ số đó khi chia cho 4 (ta gọi là \(\left(a,b,c\right)\)) phải bằng 1 trong các bộ số sau:
\(\left(0,0,0\right)\), \(\left(0,1,3\right),\left(0,2,2\right),\left(1,1,2\right),\left(3,3,2\right)\).
Với TH \(\left(a,b,c\right)\rightarrow\left(0,0,0\right)\) thì có tất cả \(C^3_4=4\) cách chọn.
Với TH \(\left(a,b,c\right)\rightarrow\left(0,1,3\right)\) thì có tất cả \(4.5^2=100\) cách chọn
Với TH \(\left(a,b,c\right)\rightarrow\left(0,2,2\right)\) thì có tất cả \(4.C^2_5=40\) cách chọn.
Với TH \(\left(a,b,c\right)\rightarrow\left(1,1,2\right)\) thì có tất cả \(C^2_5.5=50\) cách chọn.
Với TH \(\left(a,b,c\right)\rightarrow\left(3,3,2\right)\) thì có tất cả \(C^2_5.5=50\) cách chọn.
Vậy \(\left|A\right|=4+100+40+50+50=244\).
\(\Rightarrow P\left(A\right)=\dfrac{\left|A\right|}{\left|\Omega\right|}=\dfrac{244}{C^3_{19}}=\dfrac{244}{969}\).
Vậy xác suất để An chọn ra 3 quả có tổng chia hết cho 4 là \(\dfrac{244}{969}\)