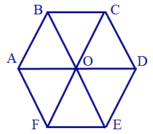
Cho mạch điện như hình vẽ. Mỗi phần đoạn mạch có điện trở R. Tính điện trở tương đương khi cho dòng điện qua mạch vào A, ra O.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điện trở tương đương: \(R=\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}=\dfrac{\left(15+25\right)10}{15+25+10}=8\Omega\)
\(U=U12=U3=12V\)(R12//R3)
\(I=U:R=12:8=1,5A\)
\(I3=U3:R3=12:10=1,2A\)
\(R1ntR2\Rightarrow I12=I1=I2\)
Mà: \(I12=I-I3=1,5-1,2=0,3A\)
\(\Rightarrow I12=I1=I2=0,3A\)

a. \(R=\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}=\dfrac{\left(80+40\right)60}{80+40+60}=40\Omega\)
b. \(U=U12=U3=IR=40.0,15=6V\)(R12//R3)
\(\left\{{}\begin{matrix}I3=U3:R3=6:60=0,1A\\I12=I1=I2=U12:R12=6:\left(80+40\right)=0,05A\left(R1ntR2\right)\end{matrix}\right.\)

a,\(R1nt\left(R2//R3\right)=>Rtd=R1+\dfrac{R2R3}{R2+R3}=4+\dfrac{6.3}{6+3}=6\left(om\right)\)
b,\(=>I1=I23=\dfrac{Uab}{Rtd}=\dfrac{9}{6}=1,5A\)
\(=>U23=I23.R23=1,5.\dfrac{6.3}{6+3}=3V=U2=U3\)
\(=>I2=\dfrac{U2}{R2}=\dfrac{3}{6}=0,5A,=>I3=\dfrac{U3}{R3}=\dfrac{3}{3}=1A\)
c,\(=>Im=Ix=I23=\dfrac{1}{3}.1,5=0,5A\)
\(=>RTd=Rx+\dfrac{R2.R3}{R2+R3}=Rx+\dfrac{6.3}{6+3}=\dfrac{U}{Im}=\dfrac{9}{0,5}=18\)
\(=>Rx=16\left(om\right)\)

a) Vào A ra D.
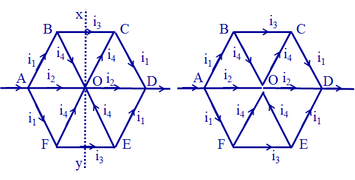
- Các đoạn mạch AB và AF; BC và FE; CD và ED đối xứng qua trục đối xứng AD.
- Các đoạn mạch AB và CD; BO và OC; AF và ED; FO và OE đối xứng qua trục đối xứng xy.
Do 2 sự đối xứng nói trên nên dòng điện qua các đoạn mạch đối xứng sẽ bằng nhau và có chiều như hình vẽ.
Vì vậy ta có thể nhả nút O mà vẫn không làm thay đổi dòng điện qua các đoạn mạch.
Ta có: R A B C O D = r + r . 2 r r + 2 r + r = 2 r + 2 r 3 = 8 r 3 ;
R A O D = 2 r ; 1 R A D = 2 . 3 8 r + 1 2 r = 10 8 r ⇒ r A D = 0 , 8 r
b) Vào A ra E.
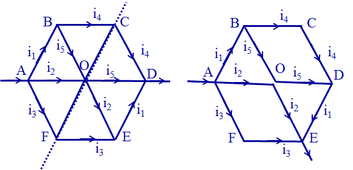
- Các đoạn mạch AB và DE; BC và CD; BO và OD; AO và OE; AF và FE đối xứng qua trục đối xứng FC, nên các dòng điện chạy qua các đoạn mạch này bằng nhau.
- Nếu xét tại nút C (hoặc F) ta thấy dòng điện qua các đoạn OC và OF bằng 0.
Vì vậy ta có thể nhả nút O mà không làm không làm thay đổi dòng điện trong mạch.
Ta có:
R A B D E = r + 2 r . 2 r 2 r + 2 r + r = 3 r ; 1 r A E = 1 2 r + 1 2 r + 1 3 r = 3 + 3 + 2 6 r = 4 3 r ⇒ r A E = 3 r 4 = 0 , 75 r .
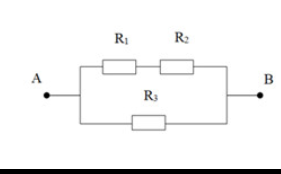


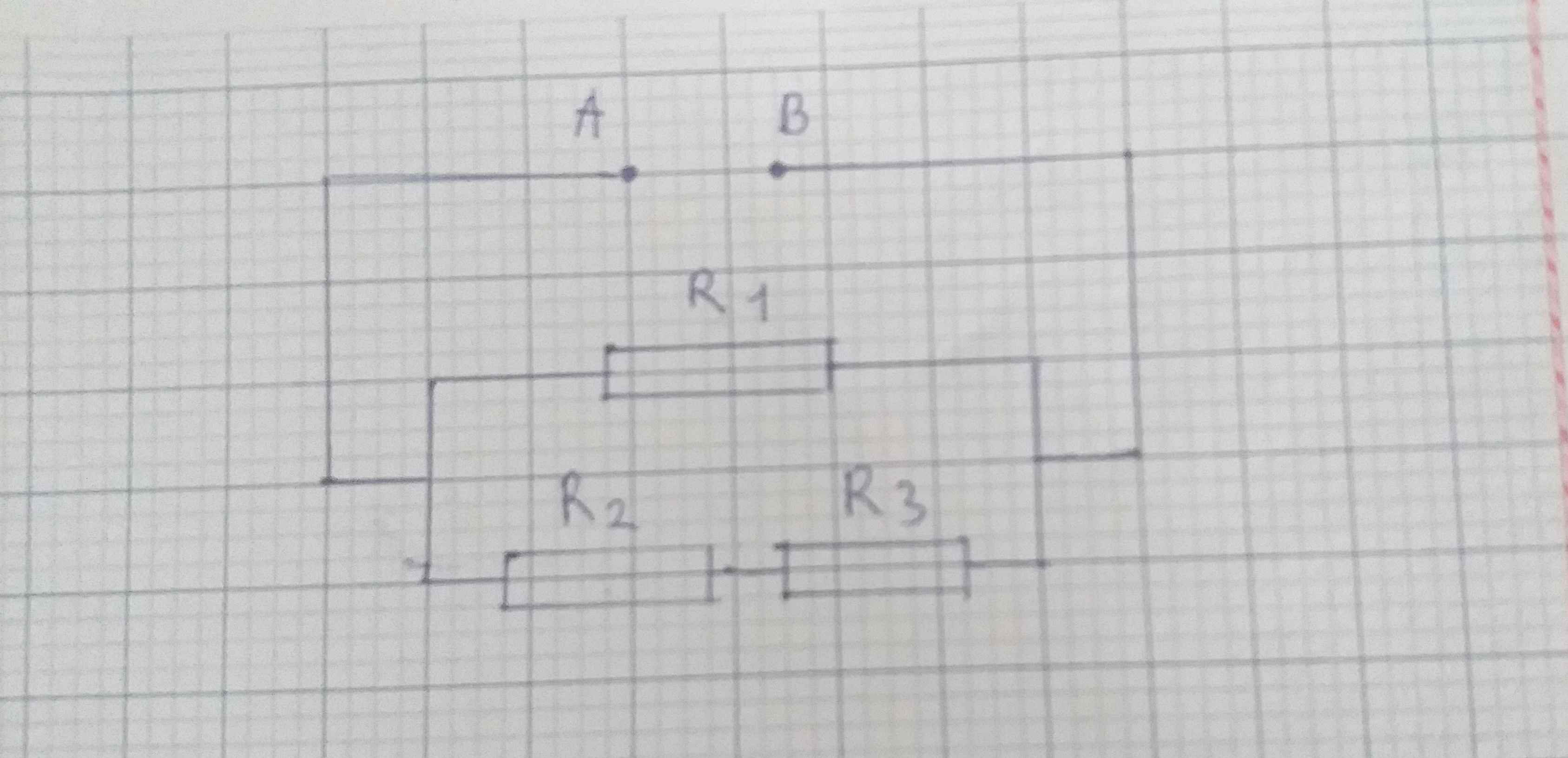 cho mạch điện như hình vẽ với R1=10 ôm , R2=4 ôm, R3=6 ôm cường độ dòng điện qua mạch chính là i = 1,5 A a) tính điện trở tương đương của mạch b) tính cường độ dòng điện qua mỗi điện trở Nhanh vs ạ e cần gấp cảm ơn nhiều ạ
cho mạch điện như hình vẽ với R1=10 ôm , R2=4 ôm, R3=6 ôm cường độ dòng điện qua mạch chính là i = 1,5 A a) tính điện trở tương đương của mạch b) tính cường độ dòng điện qua mỗi điện trở Nhanh vs ạ e cần gấp cảm ơn nhiều ạ