Trong kỳ thi học kỳ I, phòng thi số 1 có 24 học sinh trong đó có 4 học sinh tên Cương, Phát, Thịnh, Đạt. Trong phòng thi có 24 bàn sắp xếp thành 4 dãy theo hàng dọc, mỗi dãy có 6 bàn.Giám thị thi bố trí cho các học sinh ngồi ngẫu nhiên vào 24 bàn, mối bàn 1 học sinh. Tính xác suất 4 bạn có tên trên ngồi cạnh nhau theo cùng 1 hàng dọc?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Giả sử số thứ tự trong danh sách là ![]()
Do dãy này là cấp số cộng nên ta có ![]()
![]()
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố “Tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau”. Để biến cố này xảy ra ta thực hiện liên tiếp các bước sau:
Bước 1: xếp thứ tự cặp học sinh có các cặp số thứ tự là ![]()
![]()
vào trước cặp ghế đối diện nhau. Bước này có 5! cách.
Bước 2: xếp từng cặp một ngồi vào cặp ghế đối diện đã ) Chọn ở bước . Bước này có 2 5 cách.
Suy ra số kết quả thuận lợi cho biến cố A là ![]()
Vậy xác suất của biến cố A là ![]()

Chọn C.
Phương pháp:

Gọi A : “bạn Nam có đúng 2 lần ngồi vào cùng 1 vị trí”
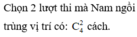
Trong 2 lượt đó, lượt đầu: Nam có 24 cách chọn vị trí, có 23! cách xếp vị trí cho 23 thí sinh còn lại; lượt sau: Nam có 1 cách chọn vị trí, có 23! cách xếp vị trí cho 23 thí sinh còn lại.
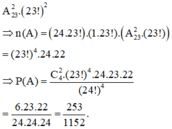

Gọi số phòng là a ta có:
a thuộc ƯCLN(96;120;75)
Ta có:
96 = 2^5 x 3
120 = 2^3 x 3 x 5
75 = 3 x 5^2
=>ƯCLN(96;120;75) = 3 x 5 = 15
Do đó chia được 15 phòng.

Có thể xếp ít nhất 3 phòng vì ước chung nhỏ nhất của 96;120;75 là 3

Gọi số học sinh dự thi là x, y là số phòng
ta có \(x=24\times y+4=26\times\left(y-1\right)\)
vậy \(24\times y+4=26\times y-26\text{ hay }y=15\)
vậy số học sinh là : \(24\times15+4=364\)

Số cách xếp 24 học sinh là 24!
Khi cho 4 bạn có tên trong đề ngồi cạnh nhau thì có 4! cách xếp
Có 4 hàng dọc, mà mỗi hàng dọc thì có 3 th là 1-2-3-4; 2-3-4-5; 3-4-5-6
=>Có 3*4*4!*20!
=>P=2/1771