Giú em tính giới hạn với ạ. Cần gấp gấp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Q
11 tháng 3 2022
- bảo quản đồ dùng học tập tốt
- quyên góp những sách vở cũ
- không viết vẽ bậy vào sách vở
- mua những loại sách cũ
- tới nhà sách thì tìm tới chỗ có khuyến mãi để mua
- mua những đồ dùng học tập cần thiết
- không đưa ra mục tiêu cụ thể
- lo lm những chuyện không liên quan
- đến sát deadline mới chịu làm
DT
Đỗ Thanh Hải
CTVVIP
5 tháng 7 2021
1 C
2 B
3 C
4 D
5 A
6 good for
7 who
8 students
9 would tell
10 to smoke
11 latest
BG
1
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
\(y=\dfrac{2x-1}{x+m}\Rightarrow y'=\dfrac{2m+1}{\left(x+m\right)^2}\)
Hàm nghịch biến trên miền xác định khi:
\(2m+1< 0\Rightarrow m< -\dfrac{1}{2}\)
KH
8 tháng 4 2020
Người ta sản xuất nhiều loại nhiệt kê với những giới hạn đo khác nhau cho từng mục đích sử dụng
vd: Đo thân nhiệt cơ thể, đo nhiệt độ của thức ăn được nấu,.......
17 tháng 6 2023
Tình hình thế giới hiện nay đang phát triển theo xu hướng hòa bình, hợp tác cùng phát triển. Nhưng đáng tiếc vẫn còn rất nhiều nơi trên thế giới vẫn đang chìm trong bom đạn của chiến tranh. Có thể kể đến một số nước Trung Đông với các phần tử khủng bố nguy hiểm đang đe doạ cuộc sống yên bình của người dân nơi đây. Vì vậy, đối với các hành động khủng bố nói riêng và phát động chiến tranh nói chung, chúng ta cần phản đối kịch liệt để giữ gìn một thế giới hạnh phúc không còn tiếng bom đạn ở bất cứ nơi đâu.
AT
3 tháng 7 2021
Bài 1:1) \(10+2\sqrt{10}=\sqrt{10}\left(2+\sqrt{10}\right)\)
2) \(7+3\sqrt{7}=\sqrt{7}\left(3+\sqrt{7}\right)\)
các câu 3,4,5 bạn làm tương tự như 2 câu trên
6) \(3a\sqrt{b}+3b\sqrt{a}=3\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)\)
7) \(a^2-2a\sqrt{2}+2=a^2-2a\sqrt{2}+\left(\sqrt{2}\right)^2=\left(a-\sqrt{2}\right)^2\)
8) \(b-4=\left(\sqrt{b}\right)^2-2^2=\left(\sqrt{b}-2\right)\left(\sqrt{b}+2\right)\)
Bài 2: 1) \(\dfrac{\left(2-\sqrt{a}\right)^2-\left(\sqrt{a}+3\right)^2}{2a+\sqrt{a}}\left(a>0\right)\)
\(=\dfrac{\left(2-\sqrt{a}-\sqrt{a}-3\right)\left(2-\sqrt{a}+\sqrt{a}+3\right)}{\sqrt{a}\left(2\sqrt{a}+1\right)}\)
\(=\dfrac{\left(-2\sqrt{a}-1\right).5}{\sqrt{a}\left(2\sqrt{a}+1\right)}=-\dfrac{5}{\sqrt{a}}\)
3) \(\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{\sqrt{a}-2}\left(a\ge0,a\ne4\right)\)
\(=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{\sqrt{a}-2}=\sqrt{a}+2-\left(2+\sqrt{a}\right)=0\)
4) \(\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(1-\dfrac{a+\sqrt{a}}{1+\sqrt{a}}\right)\left(a\ge0,a\ne1\right)\)
\(=\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{1+\sqrt{a}}\right)\)
\(=\left(1-\sqrt{a}\right)\left(1-\sqrt{a}\right)=\left(1-\sqrt{a}\right)^2=a-2\sqrt{a}+1\)
mấy câu còn lại bạn làm tương tự
3 tháng 7 2021
Bài 1:
1) \(10+2\sqrt{10}=2\sqrt{5}\left(\sqrt{5}+\sqrt{2}\right)\)
2) \(7+3\sqrt{7}=\sqrt{7}\left(\sqrt{7}+3\right)\)
3) \(5\sqrt{7}-7\sqrt{5}=\sqrt{35}\left(\sqrt{5}-\sqrt{7}\right)\)
4) \(4\sqrt{3}-2\sqrt{6}=2\sqrt{6}\left(\sqrt{2}-\sqrt{1}\right)\)
5) \(6\sqrt{6}-2\sqrt{12}+3\sqrt{2}\)
\(=\sqrt{216}-\sqrt{48}+\sqrt{18}\)
\(=\sqrt{6}\left(6-2\sqrt{2}+\sqrt{3}\right)\)
6) \(3a\sqrt{6}+36\sqrt{a}\)
\(=3\sqrt{a}\left(\sqrt{6a}+12\right)\)
\(=3\sqrt{6a}\left(\sqrt{a}+2\sqrt{6}\right)\)
7) \(a^2-2a\sqrt{2}+2=\left(a-\sqrt{2}\right)^2\)
8) \(b-4=\left(\sqrt{b}-2\right)\left(\sqrt{b}+2\right)\)
Bài 2:
a) Ta có: \(\dfrac{\left(2-\sqrt{a}\right)^2-\left(\sqrt{a}+3\right)^2}{2a+\sqrt{a}}\)
\(=\dfrac{a-4\sqrt{a}+4-a-6\sqrt{a}-9}{2a+\sqrt{a}}\)
\(=\dfrac{-10\sqrt{a}-5}{\sqrt{a}\left(2\sqrt{a}+1\right)}\)
\(=\dfrac{-5\left(2\sqrt{a}+1\right)}{\sqrt{a}\left(2\sqrt{a}+1\right)}\)
\(=-\dfrac{5}{\sqrt{a}}\)
4) Ta có: \(\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(1-\dfrac{a+\sqrt{a}}{1+\sqrt{a}}\right)\)
\(=\left(1-\sqrt{a}\right)\left(1-\sqrt{a}\right)\)
\(=a-2\sqrt{a}+1\)
29 tháng 12 2022
Các biện pháp chống ô nhiễm tiếng ồn:
- Giảm độ to của âm phát ra.
- Ngăn chặn đường truyền âm của tiếng ồn.
- Hướng âm thanh của tiếng ồn đi theo con đường khác.
- Hấp thụ tiếng ồn.
Người ta thường dùng những vật liệu cách âm (như bê tông, gạch, xốp hay bông…) để làm giảm tiếng ồn.
Để đưa ra các biện pháp chống ô nhiễm tiếng ồn trong từng trường hợp cụ thể, ta dựa vào các nguyên tắc sau:
- Làm giảm độ to của tiếng ồn phát ra.
- Ngăn chặn đường truyền âm của tiếng ồn bằng những vật liệu cách âm như bê tông, gạch, … hay trồng cây cối…
- Hấp thụ tiếng ồn bằng cách trên đường truyền của nó ta đặt những vật làm bằng xốp hay vật có hình dạng bề mặt xù xì…
- Làm cho âm truyền đi theo hướng khác….
muốn tìm hiểu thêm thì lên google có hết nhá :>>>
HN
0
LN
0
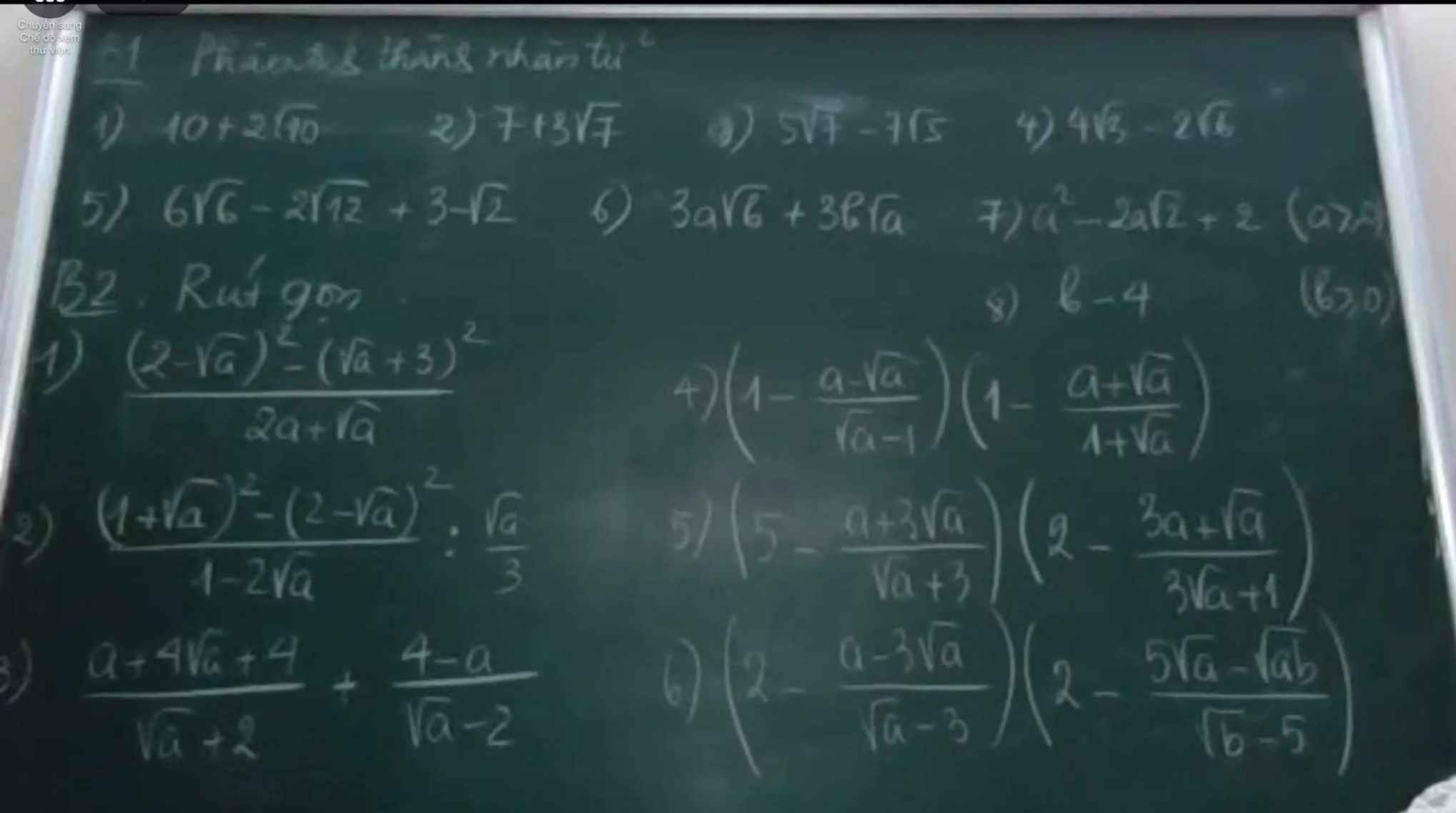
\(=lim_{x\rightarrow0}\left(\dfrac{5\cdot x\cdot\left(4x+2\right)}{5\cdot sin5x\cdot\left(\sqrt{4x^2+2x+1}+1\right)}-\dfrac{5\cdot x}{5\cdot sin5x\cdot\left(\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1\right)}\right)\)\(lim_{x\rightarrow0}\dfrac{\sqrt{4x^2+2x+1}-\sqrt[3]{x+1}}{sin5x}=lim_{x\rightarrow0}(\dfrac{\sqrt{4x^2+2x+1}-1}{sin5x}-\dfrac{\sqrt[3]{x+1}-1}{sin5x})\)\(=lim_{x\rightarrow0}\left(\dfrac{1}{\dfrac{sin5x}{5x}}\cdot\left(\dfrac{4x+2}{(\sqrt{4x^2+2x+1}+1)\cdot5}-\dfrac{1}{5\cdot\left(\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1\right)}\right)\right)\)(1)
chú ý : \(lim _{x\rightarrow0}\dfrac{1}{\dfrac{sin5x}{5x}}=\dfrac{1}{5}\)
Hay (1)= \(\dfrac{1}{5}\cdot\left(\dfrac{2}{2\cdot5}-\dfrac{1}{5\cdot3}\right)=\dfrac{2}{75}\)