Ai đó giúp mình với ạ.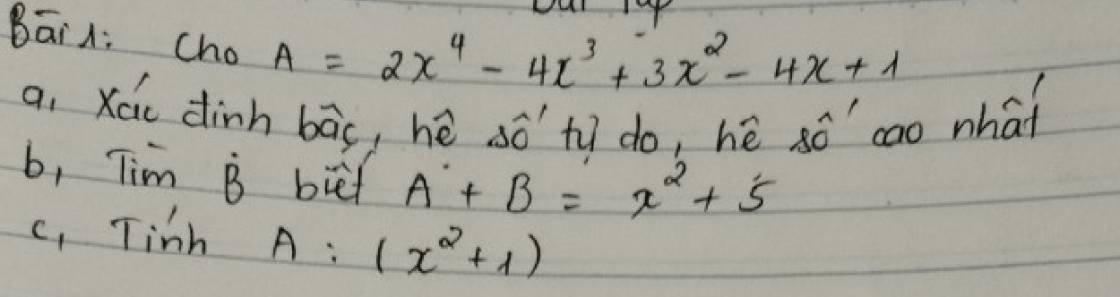
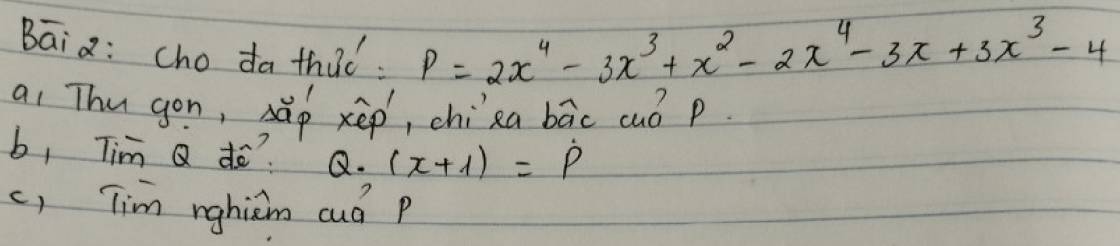
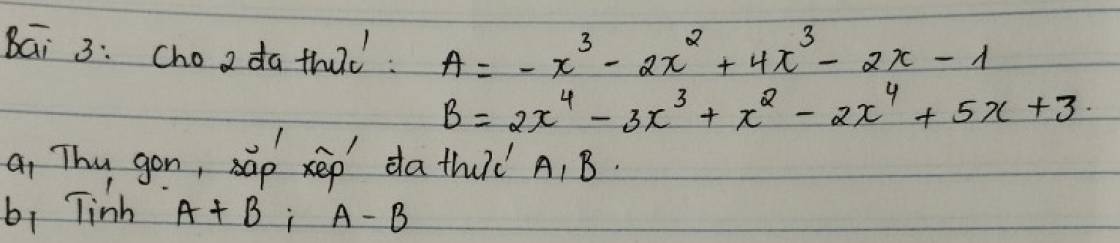
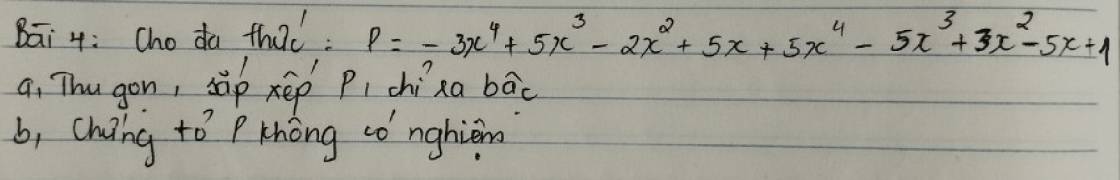
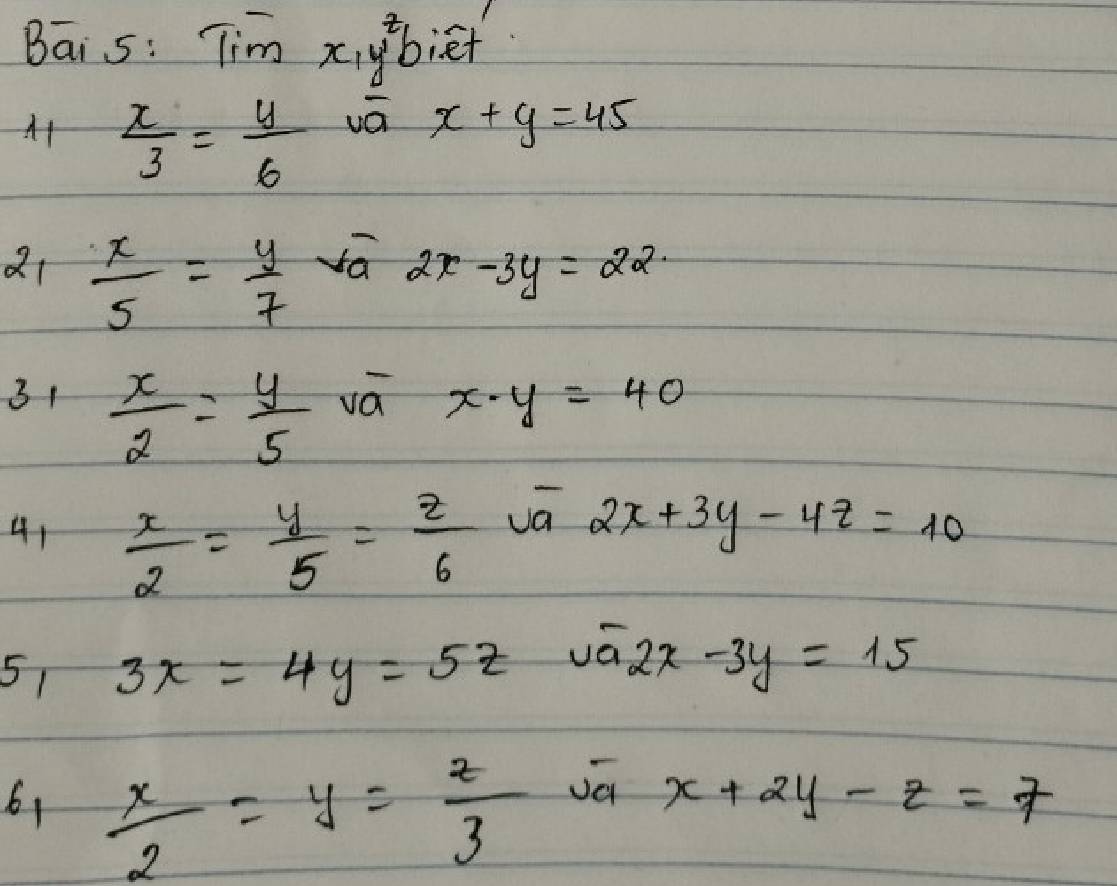
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



bài 5
a) có đa thức x2-4x+a nhận x=1 làm 1 nghiệm
=> 12-4.1+a=0
=>1-4+a=0
-3+a=0
a=3
các câu b,c,d làm tương tự
bài 6
a) có : A(x)=x2+ax+b
=>A(0)=02+a.0+b=b
mà A(0)=5
=>b=5
lại có A(x)nhận x=-1 làm 1 nghiệm
=>A(-1)=(-1)2+a.(-1)+b=0
=>1-a+b=0
=>1-a+5=0
=>a=6
b)có: B(x)=(x+2)(x+3)
cho B(x)=0
=>(x+2)(x+3)=0
=>x+2=0 hoặc x+3=0
(+)x+2=0 (+)x+3=0
x=-2 x=-3
=> nghiệm của đa thức B(x) là x=-2;x=-3
mà nghiệm của B(x) cũng là nghiệm của A(x)
=>nghiệm của đa thức A(x) là x=-2;x=-3
(*) x=-2 là nghiệm của A(x)
=>A(-2)=(-2)2+a.(-2)+b=4-2a+b=0 (1)
(*)x=-3 là nghiệm của A(x)
=>A(-3)=(-3)2+a.(-3)+b=9-3a+b=0 (2)
từ (1)và(2)=>(9-3a+b)-(4-2a+b)=0-0
=>9-3a+b-4+2a-b=0
=>5-a=0
a=5
thay a=5 vào (1) ta được:
4-5.2+b=0
4-10+b=0
-6+b=0
b=6


\(3A=3^2+3^3+...+3^{101}\)
=>\(A=\dfrac{3^{101}-3}{2}\)

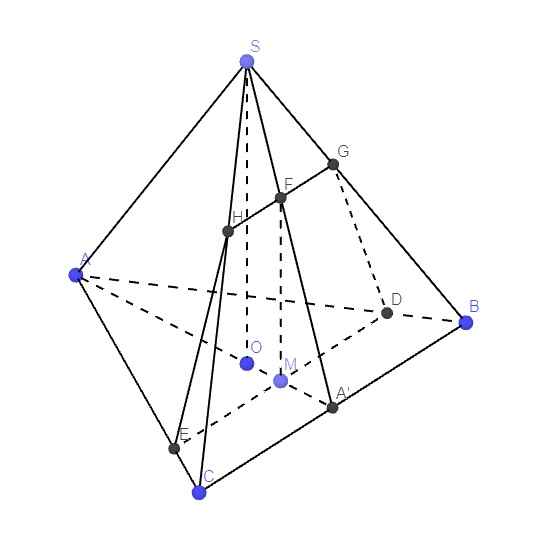
\(\left\{{}\begin{matrix}SO\perp BC\\SO\perp CA\end{matrix}\right.\) \(\Rightarrow SO\perp\left(ABC\right)\)
\(AA'=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều) \(\Rightarrow AO=\dfrac{2}{3}AA'=\dfrac{a\sqrt{3}}{3}\)
\(\Rightarrow M\) nằm trên đoạn thẳng OA'
Qua M kẻ đường thẳng song song BC cắt AB và AC lần lượt tại D và E
Trong mp (SAA'), qua M kẻ đường thẳng song song SO cắt SA' tại F
Trong mp (SBC), qua F kẻ đường thẳng song song BC cắt SB và SC lần lượt tại G và H
\(\Rightarrow\) Hình thang DEHG là thiết diện của (P) và chóp
\(FM||SO\Rightarrow FM\perp\left(ABC\right)\Rightarrow FM\perp ED\)
Áp dụng định lý Talet cho tam giác ABC:
\(\dfrac{DE}{BC}=\dfrac{AM}{AA'}\Rightarrow DE=\dfrac{BC.AM}{AA'}=\dfrac{a.x}{\dfrac{a\sqrt{3}}{2}}=\dfrac{2x\sqrt{3}}{3}\)
Talet tam giác SOA':
\(\dfrac{FM}{SO}=\dfrac{MA'}{OA'}\Rightarrow FM=\dfrac{SO.MA'}{OA'}=\dfrac{2a.\left(\dfrac{a\sqrt{3}}{2}-x\right)}{\dfrac{a\sqrt{3}}{6}}=6a-4\sqrt{3}x\)
Talet tam giác SBC:
\(\dfrac{GH}{BC}=\dfrac{SF}{SA'}=1-\dfrac{FA'}{SA'}=1-\dfrac{FM}{SO}=1-\dfrac{6a-4\sqrt{3}x}{2a}=\dfrac{2\sqrt{3}x-2a}{a}\)
\(\Rightarrow GH=2\sqrt{3}x-2a\)
\(S_{DEHG}=\dfrac{1}{2}\left(DE+GH\right).FM=\dfrac{1}{2}\left(\dfrac{2x\sqrt{3}}{3}+2\sqrt{3}x-2a\right)\left(6a-4\sqrt{3}x\right)\)
\(=\dfrac{1}{3}\left(4\sqrt{3}x-3a\right)\left(6a-4\sqrt{3}x\right)\le\dfrac{1}{12}\left(4\sqrt{3}x-3a+6a-4\sqrt{3}x\right)^2=\dfrac{9a^2}{12}\)
Dấu "=" xảy ra khi \(4\sqrt{3}x-3a=6a-4\sqrt{3}x\Leftrightarrow x=\dfrac{9a}{8\sqrt{3}}=\dfrac{3a\sqrt{3}}{8}\)


Ta có: (u.v)' = u'.v + u.v'
\(Q=80K^{\dfrac{1}{3}}\left(100-K\right)^{\dfrac{1}{2}}\)
\(Q'=80.\left(K^{\dfrac{1}{3}}\right)'.\left(100-K\right)^{\dfrac{1}{2}}+80.K^{\dfrac{1}{3}}.\left(\left(100-K\right)^{\dfrac{1}{2}}\right)'\)= \(80.\dfrac{1}{3}.K^{-\dfrac{2}{3}}.\left(100-K\right)^{\dfrac{1}{2}}+80.K^{\dfrac{1}{3}}.\dfrac{1}{2}.\left(100-K\right)^{-\dfrac{1}{2}}.\left(-1\right)\) = \(80.\left(\dfrac{\left(100-K\right)^{\dfrac{1}{2}}}{3K^{\dfrac{2}{3}}}-\dfrac{K^{\dfrac{1}{3}}}{2\left(100-K\right)^{\dfrac{1}{2}}}\right)\)= \(80.\left(\dfrac{2\left(100-K\right)^{\dfrac{1}{2}}\left(100-K\right)^{\dfrac{1}{2}}-3K^{\dfrac{2}{3}}K^{\dfrac{1}{3}}}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(80.\left(\dfrac{2\left(100-K\right)-3K}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(80.\left(\dfrac{200-5K}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(\dfrac{400\left(40-K\right)}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\) = \(\dfrac{200\left(40-K\right)}{3K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\).

\(\dfrac{x+4}{3}=\dfrac{x-11}{-6}\)
\(\dfrac{2x+8}{6}=\dfrac{-x+11}{6}\)
\(\Leftrightarrow2x+8=-x+11\)
\(\Leftrightarrow3x=3\)
\(\Leftrightarrow x=1\)
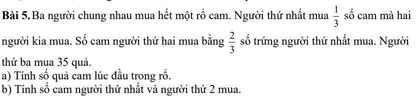




 Ai giúp mình với ạ
Ai giúp mình với ạ
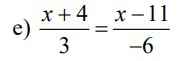
Chia từng bài ra đăng nha bạn
5: