
 Ai giải hộ mik với, ý b và câu 10 ạ
Ai giải hộ mik với, ý b và câu 10 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


10. Câu này chứng minh BĐT BSC:
\(\sqrt{\left(a^2+b^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ab+bc\right)^2}=b\left(a+c\right)\)
11.
Ta có: \(\dfrac{1}{1+a}+\dfrac{1}{1+b}-\dfrac{2}{1+\sqrt{ab}}\)
\(=\dfrac{\left(1+b\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{\left(1+a\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2\left(1+a\right)\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{1+b+\sqrt{ab}+b\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{1+a+\sqrt{ab}+a\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2+2a+2b+2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{-a-b+2\sqrt{ab}+a\sqrt{ab}+b\sqrt{ab}-2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{ab}-1\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\ge0\forall x,y\ge1\)
Đẳng thức xảy ra khi \(a=b=1\)


- Tương phản khi một vị quan phụ mẫu quyền cao chức trọng đang ngồi chơi bài trong một cái đình cao ráo, cùng với bao của ngon vật lạ, trong khi đó hàng bao người dân đang vất vả ngăn lại con lũ dữ dội bên ngoài kia
=> Tác dụng: Việc sử dụng 2 hình ảnh tương phản này góp phần nhấn mạnh thêm vào 2 điều:
1. Đời sống khổ cực của nhân dân, chịu những thiên tai dữ dội nhưng lại phải tự lo, không được sự trợ giúp của vị quan phụ mẫu
2. Sự vô tâm, không làm tròn trách nhiệm của lão quan phụ mẫu, hút máu nhân dân để sống mà không quan tâm đến nỗi khổ nhân dân, chỉ lo hưởng thụ cuộc sống giàu sang, sung túc, ăn chơi
P/s: Vì chị lớp 9 rồi nên không dám đảm bảo nhớ đúng từng chi tiết, nhưng đại ý nó là thế này


Câu 2:
1: \(9-x^2=\left(3-x\right)\left(3+x\right)\)
\(x^2-2xy+y^2-16=\left(x-y-4\right)\left(x-y+4\right)\)

Ta có \(5x=3y\Rightarrow\frac{x}{3}=\frac{y}{5}\)
Áp dụng dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{5}=\frac{x-y}{3-5}=\frac{10}{-2}=-5\)
\(\Rightarrow x=3.\left(-5\right)=-15;y=\left(-5\right).5=-25\)
Vậy x = -15 ; y = -25
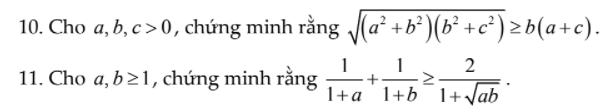 !
!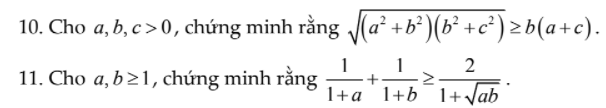
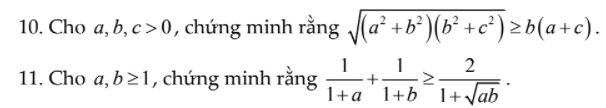








Câu 10 của em đây nhé:
\(\dfrac{17}{2}\) \(\times\) \(\dfrac{3}{5}\) + \(\dfrac{3}{5}\) \(\times\) \(\dfrac{1}{2}\) + \(\dfrac{3}{5}\)
= \(\dfrac{17}{2}\) \(\times\) \(\dfrac{3}{5}\) + \(\dfrac{3}{5}\) \(\times\) \(\dfrac{1}{2}\) + \(\dfrac{3}{5}\) \(\times\) 1
= \(\dfrac{3}{5}\) \(\times\) ( \(\dfrac{17}{2}\) + \(\dfrac{1}{2}\) + 1)
= \(\dfrac{3}{5}\) \(\times\) ( \(\dfrac{18}{2}\) + 1)
= \(\dfrac{3}{5}\) \(\times\) ( 9 + 1)
= \(\dfrac{3}{5}\) \(\times\) 10
= 6
Mn giải chi tiết giúp mik với