Cho tam giác ABC vuông tại A, đường cao AH.Gọi M,N lần lượt là trung điểm của AH,CH.
CM: a)M là trực tâm của tam giác ANB
b)BM vuông góc AN
Phần a e chưa học đường trung bình nên mong m.ng giải theo cách khác ạa!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

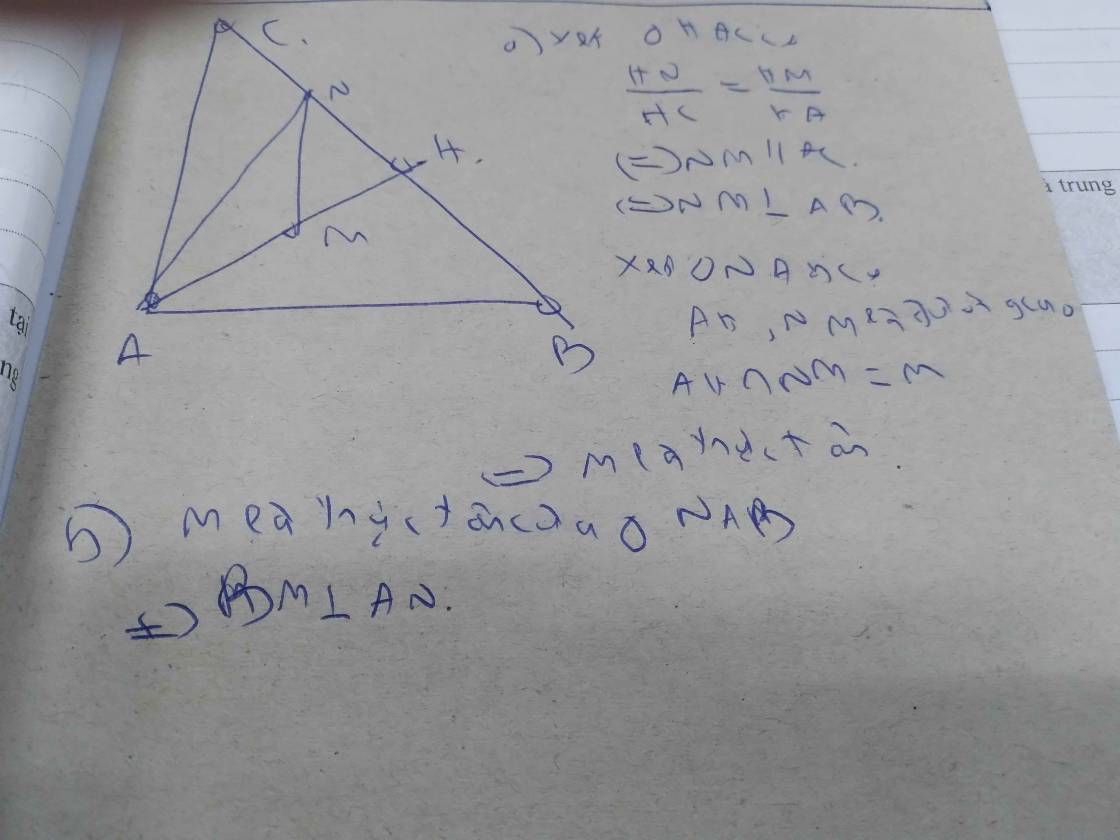

Hai tg vuông AHB~AHC => AH/BH=CH/AH=AC/AB
nhưng AH=2HM ; BH=2HN -gt- nên AV/BH=..=AC/AB=HM / HN
do đo ta có hai tg vuông CHM & AHN cũng ~ với nhau ( ~ là đồng dạng)
suy ra góc ^HAN=^HCM<=> CM và AN là hai cạnh tương ứng của hai góc =mà cặp cạnh kia CH đã vuông góc vơi AH
hoặc MN//AB ta cứ cộng các góc(=) dồn lại cũng ra ^NCM+^MNC+^MNA=!V

a: Ta có: H và M đối xứng nhau qua AB
nên AB là đường trung trực của HM
Suy ra: AH=AM(1)
Ta có: H và N đối xứng nhau qua AC
nên AC là đường trung trực của HN
Suy ra: AN=AH(2)
Từ (1) và (2) suy ra AN=AM

Xét tứ giác ADHE có :
\(\widehat{A}\)=\(\widehat{B}\)=\(\widehat{C}\)=\(\widehat{D}\)(Vì cùng =90\(^{0^{ }}\))
=) Tứ giác ADHE là hình chữ nhật
=) AH=DE (tính chất 2 đường chéo bằng nhau)
