Bài 6: Cho tam giác ABC vuông tại A, đường cao AH. Tia phân giác góc HAB cắt tia phân giác góc B tại E. Tia phân giác góc HAC cắt tia phân giác góc C tại F.
a)CMR: BE vuông góc AF
b) BE cắt CF tại K. CMR: AK vuông góc EF.
giúp tui vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\widehat{DAE}=\dfrac{1}{2}\left(\widehat{HAB}+\widehat{HAC}\right)=\dfrac{1}{2}\cdot90^0=45^0\)
b: Xét ΔAEH và ΔAEF có
AE chung
\(\widehat{HAE}=\widehat{FAE}\)
AH=AF
Do đó: ΔAEH=ΔAEF
c: Ta có: ΔAEH=ΔAEF
nên \(\widehat{AHE}=\widehat{AFE}=90^0\)
=>EF⊥AC
mà AC⊥AB
nên EF//AB

mot mieng dat hinh tam giac co day la 15m va chieu cao la 7,8m nay nguoi ta mo rong mieng dat ve ben phai bang cach keo dai canh day them 3,5m hay tinh dien h manh dat sau khi mo rong

Ta có BC^2 = AB^2 + AC^2 = 625 => BC =25
=> AH = AB.AC/BC = 20.15/25 = 12
Do tính chất phân giác, ta có:
HD/DB = AH/AB= 12/15=4/5
=> HD/DB =4/5
=> DB/HD =5/4 => HB/HD =9/4 => HD =4HB/9
Mà HB^2 = AB^2 - AH^2 = 15^2 - 12^2 =81
=> HB=9 => HD = 4 ( cm )
Tương tự ta cũng có:
Do tính chất phân giác, ta có:
HE/EC = AH/AC= 12/20=3/5
=> HE/EC =3/5
=> EC/HE =5/3 => HC/HE =8/3 => HE =3HC/8
Mà HC^2 = AC^2 - AH^2 = 20^2 - 12^2 =256
=> HC=16 => HE = 6 ( cm )
Vậy HD = 4 ( cm ) và HE = 6 ( cm )
Ta có BC^2 = AB^2 + AC^2 = 625 => BC =25
=> AH = AB.AC/BC = 20.15/25 = 12
Do tính chất phân giác, ta có:
HD/DB = AH/AB= 12/15=4/5
=> HD/DB =4/5
=> DB/HD =5/4 => HB/HD =9/4 => HD =4HB/9
Mà HB^2 = AB^2 - AH^2 = 15^2 - 12^2 =81
=> HB=9 => HD = 4
====================
Tương tự
Do tính chất phân giác, ta có:
HE/EC = AH/AC= 12/20=3/5
=> HE/EC =3/5
=> EC/HE =5/3 => HC/HE =8/3 => HE =3HC/8
Mà HC^2 = AC^2 - AH^2 = 20^2 - 12^2 =256
=> HC=16 => HE = 6

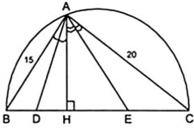
Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A, ta được:
B C 2 = A C + A B 2 ⇒ B C 2 = 15 2 + 20 2 ⇔ B C 2 = 25 2 ⇔ BC = 25( cm )
Đặt BD = x ⇒ DC = 25 - x
Áp dụng định lý Py 0 ta – go vào hai tam giác vuông AHB và AHC, ta được:
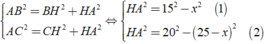
Trừ theo vế các đẳng thức ( 1 ) và ( 2 ) ta được:
15 2 - x 2 - 20 2 + ( 25 - x ) 2 = 0 ⇔ 50x = 450 ⇔ x = 9( cm )
Nên HC = 25 - 9 = 16( cm )
Thay x = 9 vào đẳng thức ( 1 ) ta có: H A 2 = 15 2 - 9 2 = 122 ⇔ HA = 12( cm )
Áp dụng tính chất đường phân giác AD vào tam giác AHB, ta được:
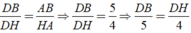
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
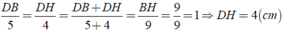
Áp dụng tính chất đường chất đường phân giác AE của tam giác ACH, ta được:
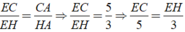
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
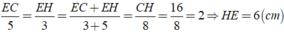

a, Xét tg BAE và tg BDE ( \(\widehat{BAE}=\widehat{BDE}=90^0\))
BA=BD (gt)
BE chung
=> tg BAE = tg BDE ( ch-cgv)
=> AE=ED
Ta có \(\hept{\begin{cases}BA=BD\left(gt\right)\\AE=ED\left(cmt\right)\end{cases}}< =>\)BE trung trực AD (đpcm)
b, +ED vuông BC
+ AH vuông BC
=> AH//DE
=> \(\widehat{HAD}=\widehat{ADE}\)( So le trong) (2)
Lại có gọi m là giao 2 đường thẳng BE và AD
vì BE trung trực AD =>+ \(\widehat{AME}=\widehat{EMD}=90^{0^{ }}\)
Xét tg AEM và tg DEM có \(\left(\widehat{AME}=\widehat{EMD}=90^0\left(cmt\right)\right)\)
+ AD = ED (cma)
+ EM chung
=> tg AEM = tg DEM ( ch-cgv)
=> \(\widehat{DAE}=\widehat{ADE}\)(2)
tỪ (1) VÀ (2) => \(\widehat{HAD}=\widehat{DAE}\)=> AD phân giác góc AHC