Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
=>ΔBAE=ΔBDE
b; BA=BD
EA=ED
=>BE là trung trực của AD

A.Xét ΔABE và ΔDBE có:
Cạnh BE chung
BD = BA
⇒ ΔABE = ΔDBE (cạnh huyền – góc nhọn)
b. Do BD = BA nên B nằm trên đường trung trực của AD
Do ΔABE = ΔDBE ⇒ AE = ED (hai cạnh tương ứng)
E nằm trên đường trung trực của AD
Vậy BE là đường trung trực của AD
c. Do ΔABE = ΔDBE ⇒ ∠(ABE) = ∠(EBC) (hai góc tương ứng)
Suy ra BE là tia phân giác của góc ABC

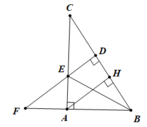
b. Do BD = BA nên B nằm trên đường trung trực của AD
Do ΔABE = ΔDBE ⇒ AE = ED (hai cạnh tương ứng) (1 điểm)
E nằm trên đường trung trực của AD (1 điểm)
Vậy BE là đường trung trực của AD (0.5 điểm)

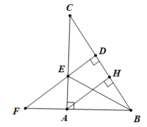
c. Do ΔABE = ΔDBE ⇒ ∠(ABE) = ∠(EBC) (hai góc tương ứng)
Suy ra BE là tia phân giác của góc ABC (1 điểm)

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
Do đó:ΔBAE=ΔBDE
Suy ra: EA=ED
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là phân giác của góc HAC
a, Xét tg BAE và tg BDE ( \(\widehat{BAE}=\widehat{BDE}=90^0\))
BA=BD (gt)
BE chung
=> tg BAE = tg BDE ( ch-cgv)
=> AE=ED
Ta có \(\hept{\begin{cases}BA=BD\left(gt\right)\\AE=ED\left(cmt\right)\end{cases}}< =>\)BE trung trực AD (đpcm)
b, +ED vuông BC
+ AH vuông BC
=> AH//DE
=> \(\widehat{HAD}=\widehat{ADE}\)( So le trong) (2)
Lại có gọi m là giao 2 đường thẳng BE và AD
vì BE trung trực AD =>+ \(\widehat{AME}=\widehat{EMD}=90^{0^{ }}\)
Xét tg AEM và tg DEM có \(\left(\widehat{AME}=\widehat{EMD}=90^0\left(cmt\right)\right)\)
+ AD = ED (cma)
+ EM chung
=> tg AEM = tg DEM ( ch-cgv)
=> \(\widehat{DAE}=\widehat{ADE}\)(2)
tỪ (1) VÀ (2) => \(\widehat{HAD}=\widehat{DAE}\)=> AD phân giác góc AHC