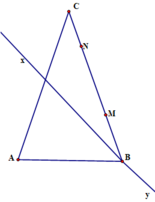
trinh bay cach ve tam giac ABC biet canh AB=5cm,BC=4cm,goc ABC =140do b)ve tia Bx la tia phân giác của góc ABC.Tính góc CBx c)chứng tỏ rằng tia Bx cắt cạnh AC của tam giác tại điểm I nằm giữa 2 điểm A và C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 4 2018
a) Có : \(\widehat{CBx}\)= 30o
\(\widehat{CBA}\) = 60O
\(\Rightarrow\)\(\widehat{CBx}\) < \(\widehat{CBA}\) ( 30o < 60o)
\(\Rightarrow\)Tia Bx nằm giữa BA, BC
\(\Rightarrow\)\(\widehat{ABx}\) + \(\widehat{CBx}\)= \(\widehat{CBA}\)
\(\Rightarrow\)\(\widehat{ABx}\) + 30o = 60o
\(\Rightarrow\)\(\widehat{ABx}\) = 60o - 30o
\(\Rightarrow\)\(\widehat{ABx}\) = 30o
b) Có : Tia Bx nằm giữa BA, BC (1)
Mà : \(\widehat{ABx}\) = 30o
\(\widehat{CBx}\) = 30o
\(\widehat{CBA}\) = 60o
\(\Rightarrow\) \(\widehat{ABx}\) = \(\widehat{CBx}\) = \(\frac{1}{2}\)\(\widehat{CBA}\) (2)
Từ (1) và (2) suy ra : Tia Bx là tia phân giác của \(\widehat{ABC}\)
