1. Cho nửa đtròn O, đkính AB. Gọi M là điểm chính giữa của cung AB, P là điểm thuộc cung MB, đthẳng AP cắt đthẳng OM tại C, đthẳng OM cắt đthẳng BP tại Da/ Cm: tứ giác OBPC nội tiếp và tích AC.AP ko đổib/ Cm: ΔBDO ∼ ΔCAOc/ Tiếp tuyến của nửa đtròn O tại P cắt CD tại I. Cm: IC = ID2. Cho nửa đtròn(O;R) đkính AB. Các điểm C và D bất kì thuộc cung AB sao cho sđ cung CD=90 độ (C ϵ cung AD). Gọi E là giao điểm của...
Đọc tiếp
1. Cho nửa đtròn O, đkính AB. Gọi M là điểm chính giữa của cung AB, P là điểm thuộc cung MB, đthẳng AP cắt đthẳng OM tại C, đthẳng OM cắt đthẳng BP tại D
a/ Cm: tứ giác OBPC nội tiếp và tích AC.AP ko đổi
b/ Cm: ΔBDO ∼ ΔCAO
c/ Tiếp tuyến của nửa đtròn O tại P cắt CD tại I. Cm: IC = ID
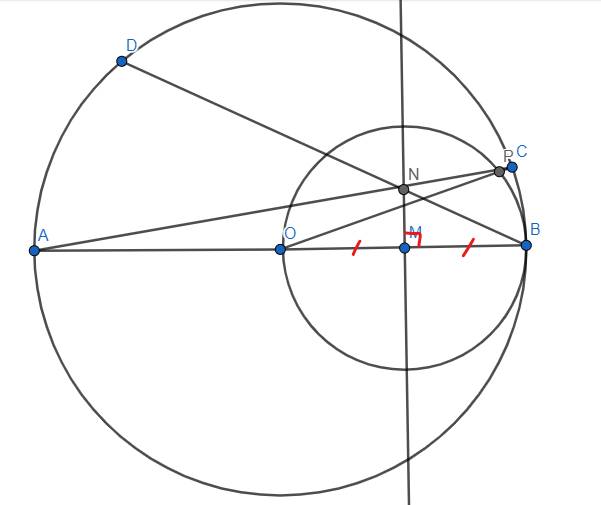
2. Cho nửa đtròn(O;R) đkính AB. Các điểm C và D bất kì thuộc cung AB sao cho sđ cung CD=90 độ (C ϵ cung AD). Gọi E là giao điểm của AC và BD, K là giao điểm của AD và BC.
a/ Tính số đo góc CED
b/ Cm: tứ giác ECKD nội tiếp và xác định tâm I của đtròn đó.
c/ Cmr: OD là tiếp tiếp của đtròn tâm I
d/ Cmr: Tổng AK.AD+BK.BC ko phụ thuộc vào vị trí 2 điểm C và D
1:
a: M là điểm chính giữa của cung AB
=>OM vuông góc AB
góc APB=1/2*sđ cung AB=90 độ
góc COB+góc CPB=180 độ
=>COBP nội tiếp
Xet ΔAOC vuông tại O và ΔAPB vuông tại P có
góc CAO chung
=>ΔAOC đồng dạng với ΔAPB
=>AO/AP=AC/AB
=>AP*AC=AO*AB=2R^2 ko đổi
b: Xét ΔBOD vuông tại O và ΔCOA vuông tại O có
góc BDO=góc CAO
=>ΔBOD đồng dạng với ΔCOA
c: góc OPI=90 độ
=>góc IPC+góc OPC=90 độ
=>góc IPC+góc PAB=90 độ
=>góc IPC=góc ACO=góc ICP
=>IC=IP và góc IDP=góc IPD
=>IC=IP=ID
=>IC=ID