cho tam giác abc vuông tại a,h thuộc ab,HEvuông góc với BCtại E ,tia EH cắt CA tạiDchứng minh CH vuông góc với BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KP
16 tháng 4 2022
trong △ BDC có :
DE⊥BC=> DE là đường cao thứ nhất của △ BDC
BA⊥CD=> BA là đường cao thứ hai của △ BDC
Mà hai đường này cắt nhau tại H
=> H là trực tâm của △ BDC
=> CH là đường cao thứ ba của △ BDC
=>CH⊥BD
11 tháng 5 2022
a: Đề sai rồi bạn
b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
Suy ra: BA=BH
c: Ta có: \(\widehat{CAH}+\widehat{BAH}=90^0\)
\(\widehat{MAH}+\widehat{BHA}=90^0\)
mà \(\widehat{BAH}=\widehat{BHA}\)
nên \(\widehat{CAH}=\widehat{MAH}\)
hay AH là tia phân giác của góc MAC
S
29 tháng 3 2023
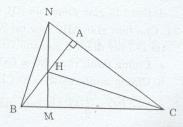
Do trong \(\Delta BNC\) có BA và NM là đường cao
Mà NM cắt BA tại H
\(\Rightarrow H\) là trực tâm của \(\Delta BNC\)
Do đó \(CH\perp NB\)
19 tháng 3 2020
a) Xét ΔABD và ΔEBD:
+) AB = BE
+) DB chung
+) ˆABD=ˆEBDABD^=EBD^ (Vì BD là phân giác)
Suy ra: ΔABD=ΔEBD (c.g.c)
- Suy ra DA = DE và DE ⊥⊥ BC
Tam giác EDC có: EC > CD – DE = CD – DA
Suy ra BC – BA > CD – DA
Có AH // DE ⇒ˆHAE=ˆAED⇒HAE^=AED^ (SLT)
Tam giác ADE cân ⇒ˆDAE=ˆAED⇒DAE^=AED^
Suy ra AE là phân giác của ˆHAC^
Kẻ EF ⊥ AC ⇒⇒ ΔAHE=ΔAFE (1)
Tam giác EFC vuông tại F ⇒ EC > EF (2)
Từ (1) và (2) ⇒ EC > HE.
P/s : hình thì tự vẽ :v
10 tháng 5 2022
a: Xét ΔAHE vuông tại E và ΔAHI vuông tại I có
AH chung
\(\widehat{EAH}=\widehat{IAH}\)
Do đó: ΔAHE=ΔAHI
Xét ΔAHN có
AE là đường cao
AE là đường trung tuyến
Do đó: ΔAHN cân tại A
b: Ta có: HN=2HE
HM=2HI
mà HE=HI
nên HN=HM
Xét ΔAHM có
AI là đường cao
AI là đường trung tuyến
DO đó: ΔAHM cân tại A
=>AH=AM=AN
Ta có: AM=AN
HM=HN
Do đó: AH là đường trung trực của MN
Anh học đến lớp 7 rồi cơ, anh siêu thật ý, anh đã 13 tuổi rồi hả anh ?em chỉ đang học lớp 2 thôi ,thêm 1 tuổi là 8 tuổi rồi , sắp lên lớp 3 rồi anh ạ .Tên anh hiện ngay ở chỗ hình tròn á ,chứ em không biết nó là cái gì.Tên anh hay thật ,Lường Tuấn Anh.Em chúc anh mạnh khỏe , luôn chăm ngoan và luôn học giỏi,tính tình tốt đẹp anh nhé!Chúc anh thực hiện được ý kiến của em nhé!Chúc anh gặp nhiều điều may mắn anh nhé!