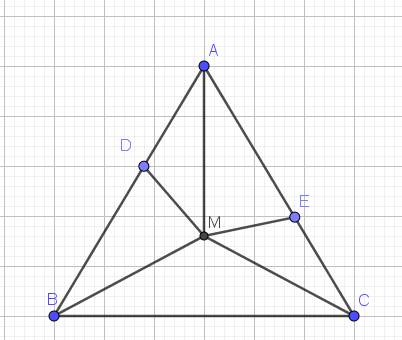
Tam giác ABC cân tại A. Đường trung trực của AB cắt BC ={M}. Lấy điểm D thuộc AB, E thuộc AC sao cho AD=CE. Cm: MD=ME
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
13 tháng 12 2022
Lời giải:
Vì $M$ nằm trên trung trực của $BC$ nên $MB=MC$. $M$ nằm trên đường trung trực của $AB$ nên $MA=MB$
$\Rightarrow MA=MB=MC$
Xét tam giác $AMC$ và $AMB$ có:
$AM$ chung
$AC=AB$ (do $ABC$ là tam giác cân tại $A$)
$MB=MC$
$\Rightarrow \triangle AMC=\triangle AMB$ (c.c.c)
$\Rightarrow \widehat{ACM}=\widehat{ABM}$
Hay $\widehat{ECM}=\widehat{ABM}$
Mà $\widehat{ABM}=\widehat{MAB}$ (do tam giác $MAB$ cân tại $M$ vì $MA=MB$)
$\Rightarrow \widehat{ECM}=\widehat{MAB}=\widehat{DAM}$
Xét tam giác $ECM$ và $DAM$ có:
$EC=DA$ (gt)
$\widehat{ECM}=\widehat{DAM}$ (cmt)
$CM=AM$ (cmt)
$\Rightarrow \triangle ECM=\triangle DAM$ (c.g.c)
$\Rightarrow ME=MD$ (đpcm)
18 tháng 6 2023
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc BAD chung
=>ΔADB=ΔAEC
=>BD=CE
b: góc ABD=góc ACE
=>góc HBC=góc HCB
=>ΔHBC cân tại H
c: AB=AC
HB=HC
=>AH là trung trực của BC
30 tháng 6 2023
a:
ΔABC cân tại A có AH là đường cao
nên AH là trung trực của BC
I nằm trên trung trực của AB
=>IA=IB
I nằm trên trung trực của BC
=>IB=IC
=>IA=IC
b: IA=IC
=>góc IAC=góc ICA
=>góc ICE=góc IAD
Xét ΔIEC và ΔIDA có
CE=DA
góc ICE=góc IAD
IC=IA
=>ΔIEC=ΔIDA
=>IE=ID
