Cho ∆ABC vuông tại A, đường cao AH, H €BCa) chứng minh∆ ABC đồng dạng ∆HACb) chứng minh ∆HBA đồng dạng ∆HAC từ đó suy ra AH²=BH.HCc) kẻ đường phân giác BE của ∆ABC (E€AC). Biết BH=9 cm, HC=16cm, tính độ dài các đoạn thẳng AE,ECd) trong∆ AEB kẻ phân giác EM (M€AB). Trong ∆BEC kẻ đường phân giác EN (N€BC). Chứng minh rằng...
Đọc tiếp
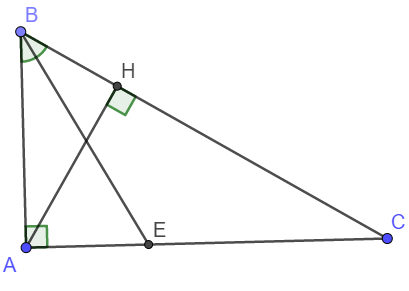
Cho ∆ABC vuông tại A, đường cao AH, H €BC
a) chứng minh∆ ABC đồng dạng ∆HAC
b) chứng minh ∆HBA đồng dạng ∆HAC từ đó suy ra AH²=BH.HC
c) kẻ đường phân giác BE của ∆ABC (E€AC). Biết BH=9 cm, HC=16cm, tính độ dài các đoạn thẳng AE,EC
d) trong∆ AEB kẻ phân giác EM (M€AB). Trong ∆BEC kẻ đường phân giác EN (N€BC). Chứng minh rằng (BM/MA).(AE.EC).(CN/BN)=1
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đòng dạng với ΔHAC
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC
c: \(AB=\sqrt{9\cdot25}=15\left(cm\right)\)
AC=căn 16*25=20(cm)
BE là phân giác
=>AE/AB=CE/BC
=>AE/3=CE/5=(AE+CE)/(3+5)=20/8=2,5
=>AE=7,5cm; CE=12,5cm