Cho tam giác ABC có ba góc nhọc (AB<AC). Lấy hai điểm E,F nằm ngoài tam giác ABC so cho AE vuông góc với AB, AF vuông góc với AC và AE = AB, AF = AC. Gọi I,O lần lượt là giao điểm của BF với AC, EC.
a) chứng minh tam giác AEC= tam giác ABF
b) chứng minh BF vuông góc với CE
c) kẻ AH vuông góc với BC(H thuộc BC), EN và FN cùng vuông góc với AH(M,N thuộc AH)
chứng minh EM=FN

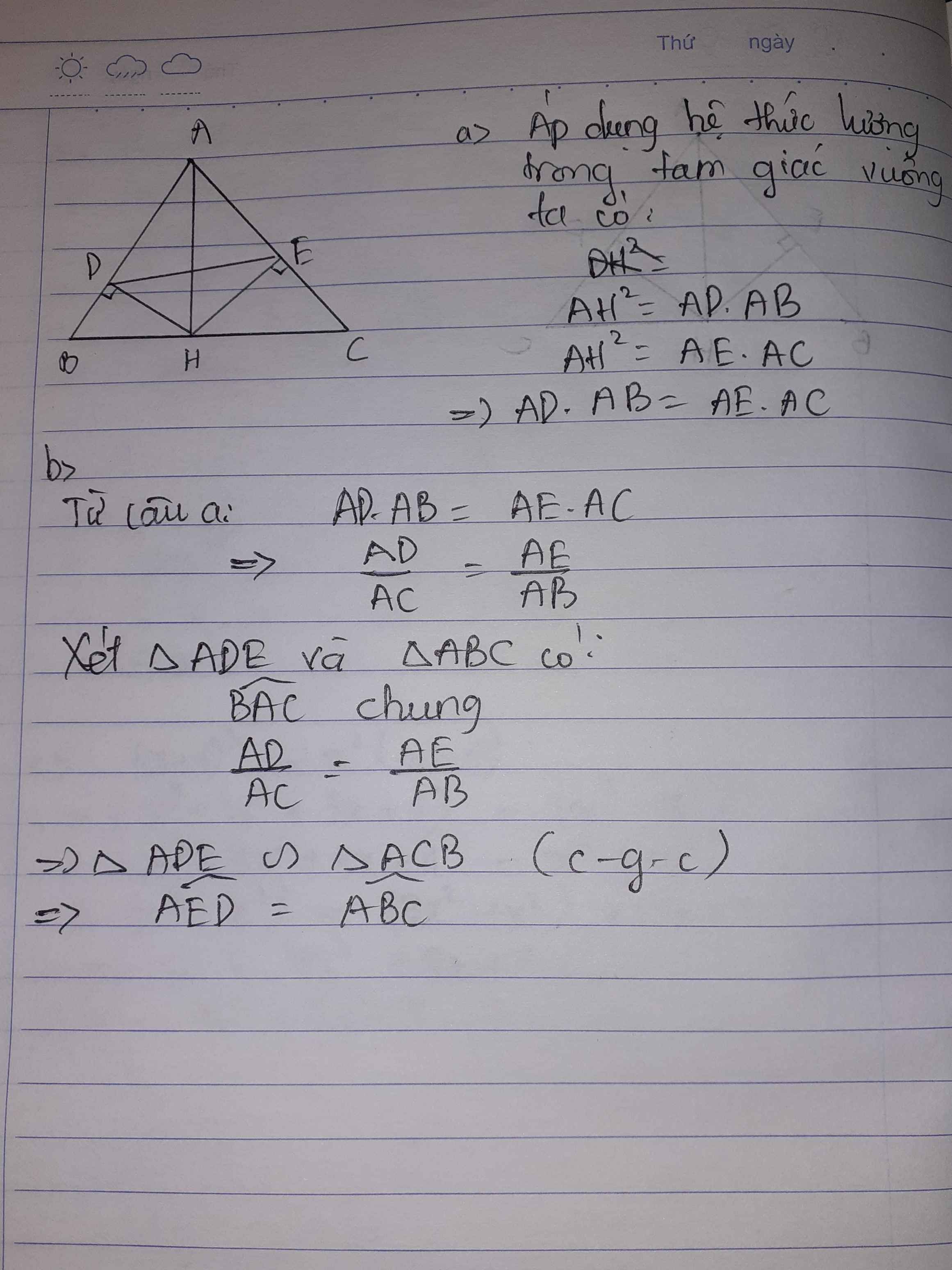
a: Xét ΔAEC và ΔABF có
AE=AB
góc EAC=góc BAF
AC=AF
=>ΔAEC=ΔABF
b: góc F+góc E=45+45=90 độ
=>góc FIE=90 độ
=>BF vuông góc CE