
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên


NT
0


19 tháng 8 2021
a: Xét ΔBAC có
AD là đường cao ứng với cạnh BC
BE là đường cao ứng với cạnh AC
AD cắt BE tại H
Do đó: H là trực tâm của ΔBAC
Suy ra: CH\(\perp\)AB tại F
Xét ΔFAH vuông tại F và ΔFCB vuông tại F có
\(\widehat{FAH}=\widehat{FCB}\left(=90^0-\widehat{FBC}\right)\)
Do đó: ΔFAH\(\sim\)ΔFCB

27 tháng 5 2023
a: sin ACB=AH/AC
=>AH/AC=1/2
=>AH=4cm
b: sin ABC=2/3
=>AH/AB=2/3
=>AB=6cm
HB=căn 6^2-4^2=2căn 5cm
HC=căn 8^2-4^2=4căn 3cm
BC=HB+HC=2căn5+4căn3(cm)
S ABC=1/2*BA*BC*sinB
=1/2*1/2*6*(2căn5+4căn3)
=3(căn 5+2căn 3)
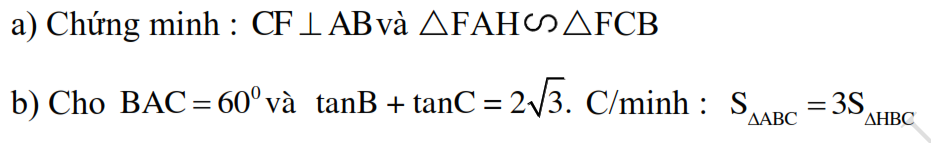
thiếu đề