Cho tam giác ABC vuông tại C có ABC = 60° Dựng tam giác cân BEC ra phía ngoài tam giác ABC sao cho BEC = 150°. Gọi D là điểm đối xứng với C qua AB, F là giao điểm của AB và DE, G là giao điểm của AB và CD.
1) Chứng minh tứ giác ABEC nội tiếp.
2) Tính số đo góc BED.
3) Chứng minh hai đường thẳng BC và FG song song.

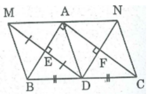


1: Xét tứ giác ABEC có
góc A+góc E=180 độ
=>ABEC là tứgiác nội tiếp
2: Vì ABEC là tứ giác nội tiếp
nên E nằm trên đường tròn đường kính BC
=>góc BED=90 độ-góc ABC=30 độ
3: Vì EB=EC
nên góc CDE=góc EAB
=>góc GDF=góc GAF
=>AGFD là tứ giác nội tiếp
=>góc DGF=góc DAF
=>góc DAB=góc DCB
=>GF//BC