Cminh rằng trong 1 tam giác cân độ dài đoạn thẳng nối đỉnh đối diện với đáy và 1 điểm bất kì của cạnh đáy nhỏ hơn hoặc = độ dài của cạnh bên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 1 2017
Nếu: \(\Delta ABC\)cân tại a, M là điểm thuộc cạnh đáy BC, ta chứng minh \(AM\le AB\), \(AM\le AC\)
+ Nếu M = A hoặc M = B ( kí hiệu đọc là trùng với ) thì AM = AB ư, AM = AC
+ Nếu M nằm giữa B và C; ( M \(\ne\)B, C ). Gọi H là trung điểm của BC, mà \(\Delta\)ABC cân tại a nên AH \(⊥\)BC
+ Nếu M = H \(\Rightarrow\)AM \(⊥\)BC \(\Rightarrow\)AM < AB và AM < AC
+ Nếu M \(\ne\)K giả sử M nằm giữa H và C \(\Rightarrow\)MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA \(\Rightarrow\)MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM \(\le\)AB, AM \(\le\)AC
19 tháng 4 2017
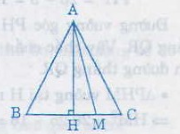
Giả sử ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC
tam giác ABC cân tại A, M thuộc CH. H là trung điểm CB
Ta có 90o > \(\widehat{HAC}\) > \(\widehat{HAM}\)
=> cos(\(\widehat{HAC}\)) < cos(\(\widehat{HAM}\))
<=> \(\frac{AH}{AC}\) < \(\frac{AH}{AM}\)
=> AM < AC