Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

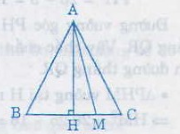
Giả sử ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC

Giả sử ΔABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB; AM ≤ AC.
- TH1 : Nếu M ≡ B hoặc M ≡ C (Kí hiệu đọc là trùng với) thì AM = AB = AC.
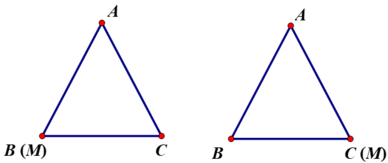
- TH2 : Nếu M nằm giữa B và C và M ≠ B; M ≠ C.
Kẻ AH ⊥ BC tại H
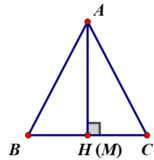
+ Nếu M ≡ H ⇒ AM ⊥ BC tại M hay AM là đường vuông góc từ A đến BC.
Mà AB, AC là các đường xiên từ A đến đường thẳng BC.
Theo định lí 1 : Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường thẳng vuông góc là đường ngắn nhất.
⇒ AM < AB và AM < AC.
+ Nếu M ≠ H giả sử M nằm giữa H và C ⇒ MH < CH.
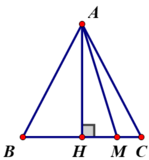
Vì MH và CH lần lượt là hình chiếu của đường xiên MA và CA trên đường BC
Mà MH < CH ⇒ MA < CA (đường xiên nào có hình chiếu lớn hơn thì lớn hơn).
Chứng minh tương tự nếu M nằm giữa H và B
Vậy mọi vị trí của M trên cạnh đáy BC thì AM ≤ AB = AC.
Các bn ơi! Giup mk với