Cho tam giác ABC ( AB < AC). AD là phân giác.Trên tia đối của tia Da lấy M: \(\widehat{DCM}\)= \(\widehat{BAD}\).
a) CMR: AB.DM = DB.CM
b) tam giác ABD đồng dạng với tam giác AMC
c) AD2 = AB.AC - DB.DC
d) Gọi BE, CF là đường phân giác của tam giác ABC. CMR: \(\frac{AF}{BF}\). \(\frac{BD}{CD}\). \(\frac{CE}{AE}\)= 1

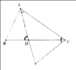
a) Xét tam giác BAD và tam giác MCD có:
góc BAD = MCD (gt)
góc ADB = CDM (2 góc đối đỉnh)
=> 2 tam giác trên đồng dạng => AB/CM = DB/DM => AB.DM = DB.CM
b) Tam giác BAD đồng dạng vói MCD (cmt) => góc ABD = CMD
Xét tam giác ABD và AMC có: góc BAD = MAC (gt)
góc ABD = ACM (cmt)
=> 2 tam giác trên đồng dạng
Còn ý d bạn dùng định lý Ceva nha.
chủ yếu là ý c thôi