trên trục tọa độ Oxy cho đường thẳng d: 3x-2y+5=0 và A(4;7),B(2;1)
Tìm tọa độ điểm M thuộc d sao cho : giá trị tuyệt đối của MA-2MB nhỏ nhất
(MA và MB đều là vecto nhá)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 2 2021
1. Gọi d' là đường thẳng qua A và vuông góc d
\(\Rightarrow\) d' nhận (1;3) là 1 vtpt
Phương trình d':
\(1\left(x+2\right)+3\left(y-3\right)=0\Leftrightarrow x+3y-4=0\)
H là giao điểm d và d' nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}3x-y+4=0\\x+3y-4=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{4}{5}\\y=\dfrac{8}{5}\end{matrix}\right.\)
\(\Rightarrow H\left(-\dfrac{4}{5};\dfrac{8}{5}\right)\)
2.
Do A' đối xứng A qua d nên H là trung điểm AA'
\(\Rightarrow\left\{{}\begin{matrix}x_{A'}=2x_H-x_A=\dfrac{2}{5}\\y_{A'}=2y_H-y_A=\dfrac{1}{5}\end{matrix}\right.\)
\(\Rightarrow A'\left(\dfrac{2}{5};\dfrac{1}{5}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 2 2021
3.
Gọi B là giao điểm d và \(\Delta\) thì tọa độ B thỏa mãn:
\(\left\{{}\begin{matrix}3x-y+4=0\\x+2y-5=0\end{matrix}\right.\) \(\Rightarrow B\left(-\dfrac{3}{7};\dfrac{19}{7}\right)\)
Lấy điểm \(C\left(0;4\right)\) thuộc d
Phương trình đường thẳng \(d_1\) qua C và vuông góc \(\Delta\) có dạng:
\(2\left(x-0\right)-\left(y-4\right)=0\Leftrightarrow2x-y+4=0\)
Gọi D là giao điểm \(\Delta\) và \(d_1\Rightarrow\left\{{}\begin{matrix}x+2y-5=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow D\left(-\dfrac{3}{5};\dfrac{14}{5}\right)\)
Gọi D' là điểm đối xứng C qua \(\Delta\Rightarrow\) D là trung điểm CD'
\(\Rightarrow\left\{{}\begin{matrix}x_{D'}=2x_D-x_C=-\dfrac{6}{5}\\y_{D'}=2y_D-y_C=\dfrac{8}{5}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{BD'}=\left(-\dfrac{27}{35};-\dfrac{39}{35}\right)=-\dfrac{3}{35}\left(9;13\right)\)
Phương trình đường thẳng đối xứng d qua denta (nhận \(\left(9;13\right)\) là 1 vtcp và đi qua D':
\(\left\{{}\begin{matrix}x=-\dfrac{6}{5}+9t\\y=\dfrac{8}{5}+13t\end{matrix}\right.\)
CM
30 tháng 11 2017
Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox .
Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:
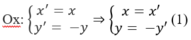
Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0.
Từ đó suy ra phương trình của d' là 3x − 2y – 6 = 0
Thay (1) vào phương trình của (C) ta được x ' 2 + y ' 2 − 2 x ′ + 4 y ′ − 4 = 0 .
Từ đó suy ra phương trình của (C') là x − 1 2 + y − 2 2 = 9 .
Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3,
từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là x − 1 2 + y − 2 2 = 9
CM
26 tháng 2 2017
Đáp án B
Do điểm M nằm trên trục hoành nên M( x; 0)
Khoảng cách từ M đến mỗi đường thẳng lần lượt là:
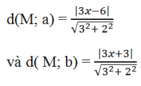
Theo bài ra ta có: d( M; a) = d( M; b) nên
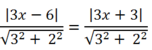
Do đó: 
Sut ra 3x- 6= -3x-3 nên x= 1/2
Vậy điểm M ( 1/2; 0)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
Cách 1:
Do M thuộc d, gọi tọa độ M có dạng \(M\left(2m-2;m\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(2m-2;m-6\right)\\\overrightarrow{BM}=\left(2m-4;m-5\right)\end{matrix}\right.\)
Đặt \(T=MA+MB=\sqrt{\left(2m-2\right)^2+\left(m-6\right)^2}+\sqrt{\left(2m-4\right)^2+\left(m-5\right)^2}\)
\(T=\sqrt{5m^2-20m+40}+\sqrt{5m^2-26m+41}\)
\(T=\sqrt{5\left(m-2\right)^2+\left(2\sqrt{5}\right)^2}+\sqrt{5\left(\dfrac{13}{5}-m\right)^2+\left(\dfrac{6}{\sqrt{5}}\right)^2}\)
\(T\ge\sqrt{5\left(m-2+\dfrac{13}{5}-m\right)^2+\left(2\sqrt{5}+\dfrac{6}{\sqrt{5}}\right)^2}=\sqrt{53}\)
Dấu "=" xảy ra khi và chỉ khi:
\(6\left(m-2\right)=10\left(\dfrac{13}{5}-m\right)\Leftrightarrow m=\dfrac{19}{8}\)
\(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2020
Cách 2:
Thay tọa độ A và B vào pt (d) được 2 giá trị cùng dấu âm \(\Rightarrow A;B\) nằm cùng phía so với (d)
Gọi d' là đường thẳng qua A và vuông góc với d \(\Rightarrow\) pt d' có dạng:
\(2\left(x-0\right)+1\left(y-6\right)=0\Leftrightarrow2x+y-6=0\)
Gọi C là giao điểm của d và d' \(\Rightarrow\left\{{}\begin{matrix}x-2y+2=0\\2x+y-6=0\end{matrix}\right.\)
\(\Rightarrow C\left(2;2\right)\)
Gọi D là điểm đối xứng với A qua d \(\Leftrightarrow C\) là trung điểm AD \(\Rightarrow D\left(4;-2\right)\)
Phương trình BD có dạng: \(7\left(x-2\right)+2\left(y-5\right)=0\Leftrightarrow7x+2y-24=0\)
\(MA+MB\) nhỏ nhất khi và chỉ khi M là giao điểm của BD
\(\Rightarrow\) Tọa độ M thỏa mãn: \(\left\{{}\begin{matrix}7x+2y-24=0\\x-2y+2=0\end{matrix}\right.\) \(\Rightarrow M\left(\dfrac{11}{4};\dfrac{19}{8}\right)\)
MN
23 tháng 5 2020
\(\overrightarrow{n_{d1}}=\left(1;2\right)\) ; \(\overrightarrow{n_{d2}}=\left(3;m\right)\)
Ta có: cos(d1;d2) = \(\left|cos(\overrightarrow{n_{d1};}\overrightarrow{n_{d2}})\right|\) = \(\frac{\sqrt{2}}{2}\)
=> \(\frac{3+2m}{\sqrt{\left(3+m^2\right)5}}\) = \(\frac{\sqrt{2}}{2}\) ⇔ 2(3 + 2m) = \(\sqrt{10\left(3+m^2\right)}\)
=> ĐK: 3 + 2m > 0 ⇔ m > \(\frac{-3}{2}\)
Gọi `M(x;3/2x+5/2)`
Ta có:`|\vec{MA}-2\vec{MB}|`
`=|(4-x;7-3/2x-5/2)-2(2-x;1-3/2x-5/2)|`
`=|(x;3/2x+17/2)|`
`=\sqrt{x^2+(3/2x+17/2)^2}`
`=\sqrt{x^2+9/4x^2+51/2x+289/4}`
`=\sqrt{13/4x^2+51/2x+289/4}`
`=\sqrt{(\sqrt{13}/2 x+[51\sqrt{13}]/26)^2+289/13} >= [17\sqrt{13}]/13`
Dấu "`=`" xảy ra `<=>\sqrt{13}/2x+[51\sqrt{13}]/26=0<=>x=-51/13`
`=>M(-51/13;-44/13)`