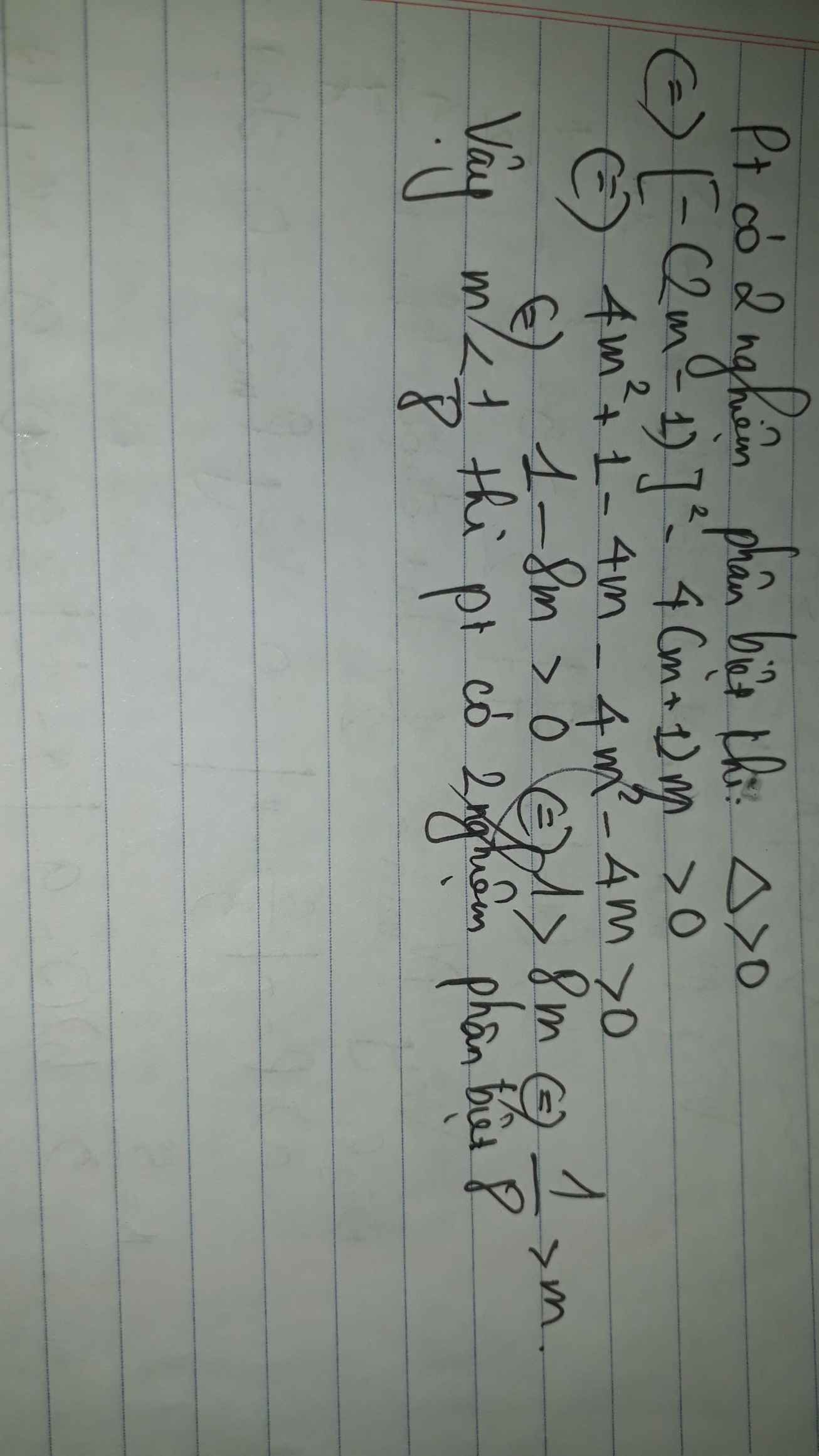1) Cho phương trình ẩn x, tham số n \(\varepsilon\)N:
1 + 1/10(x - 1) + 2 + 1/10(x - 2) + 3 + 1/10(x - 3) + ........ + n +1/10(x - n) = x
a) Tìm điều kiện của n để phương trình có ngiệm x>0;
b) Với các giá trị nào của n thì phương trình có nghiệm nguyên, dương. Tìm các nghiệm đó.
2) Rút gọn biểu thức sau:
A = (x3 - y3){\(\frac{x^2+xy}{x^2+xy+y^2}\)- [\(\frac{x\left(2x^2+xy-y^2\right)}{x^3-y^3}-2+\frac{y}{y-x}\)]:[\(\frac{x-y}{x}-\frac{x}{x-y}\)]}
3) Tìm các số a, b để đa thức P(x) luôn chia hết cho đa thức Q(x) với:
P(x) = 6x4 - 7x3 + ax2 + 3x + 2
Q(x) = x2 - x + b
4) Xác định đa thức bậc ba F(x). Biết F(0) = 8; F(1) = 20; F(2) = 2; F(3) = 2004:
F(x) = ax(x - 1)(x - 2) + bx(x - 1) + cx + d
5) C/m rằng: Hiệu các bình phương của 2 số tự nhiên lẻ bất kì luôn chia hết cho 8
6) Cho biểu thức M = \(\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}\)và B = \(\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{x+y}\)
a) Chứng minh rằng nếu A = 1 thì B = 0.
b) Ngược lại nếu B =0 thì A = 0 có đúng không? Vì sao?
- The End -