Tìm các số nguyền x;y thỏa mãn điều kiện:
xy-2x+3y=5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 8 2018
ta có: \(\frac{3x-31}{x-6}=\frac{3x-18-13}{x-6}=\frac{3.\left(x-6\right)-13}{x-6}=3-\frac{13}{x-6}\)
Để 3x-31/x-6 thuộc Z
=> 13/x-6 thuộc Z
=> 13 chia hết cho x - 6
=> x - 6 thuộc Ư(13)={1;-1;13;-13}
nếu x - 6 = 1 => x = 7
...
bn tự xét típ nha!
ML
26 tháng 2 2021
Program Hoc24;
var a: array[1..32000] of integer;
d,i,n,x: integer;
begin
write('Nhap N: '); readln(n);
for i:=1 to n do
begin
write('Nhap so thu ',i,': '); readln(a[i]);
end;
write('Nhap so can tim: '); readln(x);
d:=0;
for i:=1 to n do if a[i]=x then d:=d+1;
if d>0 then write('Co so can tim trong day ban dau') else write('Khong co so can tim trong day ban dau');
readln
end.
26 tháng 2 2021
uses crt;
var a:array[1..100]of integer;
n,i,x,kt:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
write('Nhap so can tim: '); readln(x);
kt:=0;
for i:=1 to n do
if a[i]=x then kt:=1;
if kt=0 then writeln(x,' khong co trong day')
else writeln(x,' co trong day');
readln;
end.
1 tháng 3 2020
ĐKXĐ: \(x\ne-1\) , \(x\ne3\)
Đặt A = \(\frac{2x}{\left(x+1\right)\left(x-3\right)}\)
\(=\frac{2x}{x^2-3x+x-3}=\frac{2x}{x^2-2x-3}=\frac{2x}{2x\left(\frac{x}{2}-1-\frac{3}{2x}\right)}\)
\(=\frac{1}{\frac{x}{2}-1-\frac{3}{2x}}=\frac{1}{\frac{1}{2}\left(x-\frac{3}{x}\right)-1}\)
Vì A có giá trị nguyên nên: \(1⋮\frac{1}{2}\left(x-\frac{3}{x}\right)-1\)
\(\Leftrightarrow\frac{1}{2}\left(x-\frac{3}{x}\right)-1\inƯ\left(1\right)=\left\{\pm1\right\}\)
TH1: \(\frac{1}{2}\left(x-\frac{3}{x}\right)-1=1\Leftrightarrow\frac{1}{2}\left(x-\frac{3}{x}\right)=2\)
\(\Leftrightarrow x-\frac{3}{x}=4\Leftrightarrow\frac{x^2-3}{x}=4\Leftrightarrow x^2-3=4x\)
\(\Leftrightarrow x^2-3-4x=0\Leftrightarrow\left(x^2-4x+4\right)-7=0\Leftrightarrow\left(x-2\right)^2-7=0\)
\(\Leftrightarrow\left(x-2\right)^2=7\)
\(\Leftrightarrow x-2=\sqrt{7}\Leftrightarrow x=\sqrt{7}+2\left(tm\right)\)
TH2: \(\frac{1}{2}\left(x-\frac{3}{x}\right)-1=-1\Leftrightarrow\frac{1}{2}\left(x-\frac{3}{x}\right)=0\)
\(\Leftrightarrow x-\frac{3}{x}=0\Leftrightarrow x=\frac{3}{x}\Leftrightarrow x^2=3\Rightarrow x=\sqrt{3}\left(tm\right)\)
Vậy để biểu thức có giá trị nguyên thì \(\hept{\begin{cases}x=\sqrt{7}+2\\x=\sqrt{3}\end{cases}}\)
LD
11 tháng 3 2022
Câu 1 : Tham khảo : Loigiaihay
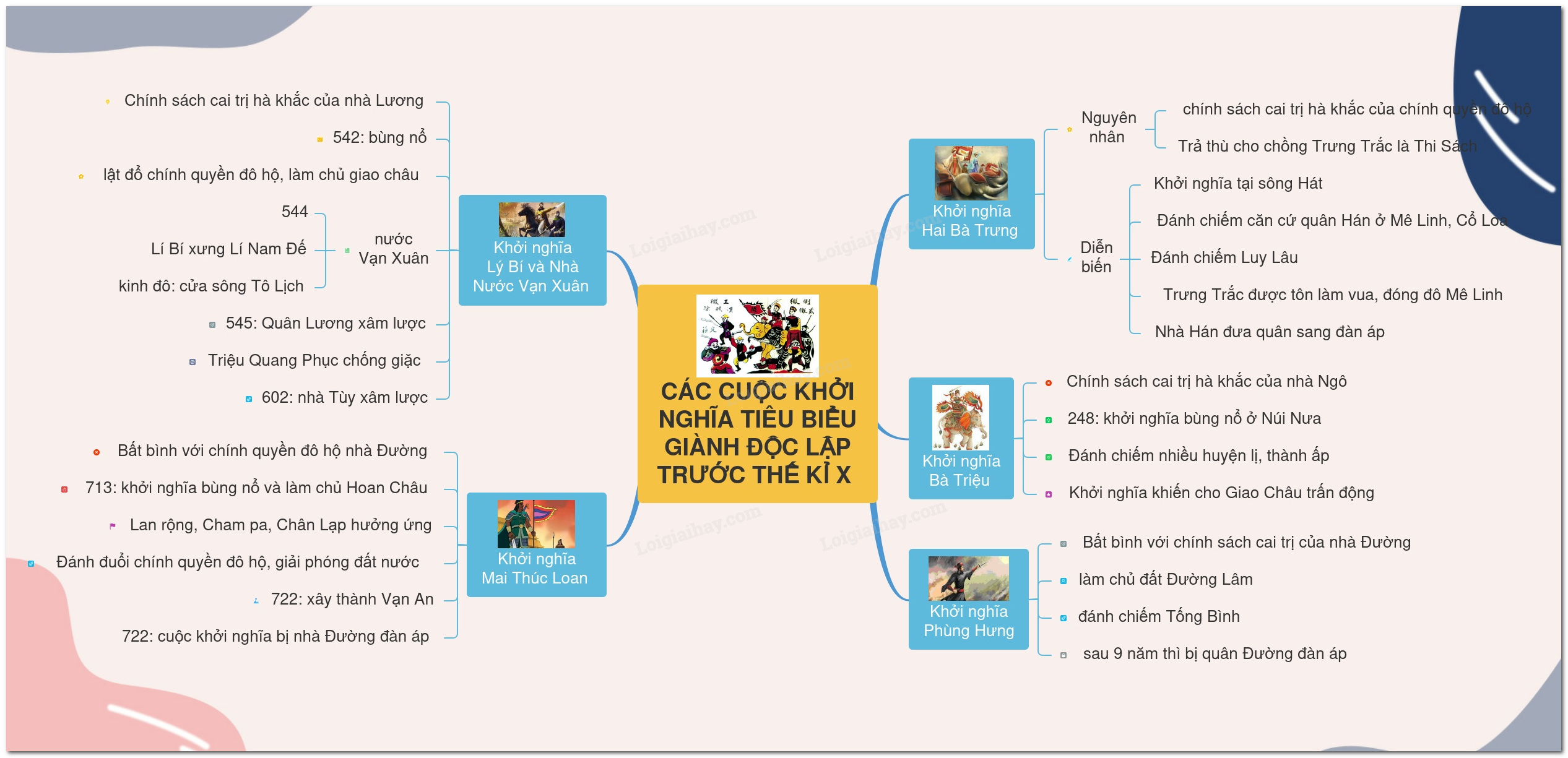
Câu 2 :
- Đều diễn ra sôi nổi, quyết liệt và bền bỉ; hàng trăm cuộc khởi nghĩa lớn nhỏ đã diễn ra, thu hút sự tham gia của đông đảo các tầng lớp nhân dân.
- Thể hiện tinh thần yêu nước, ý chí bất khuất; đoàn kết đấu tranh của người Việt.
Câu 3 :
- Người xưa thường nói "tiếng ta còn thì đất ta còn" có nghĩa là nếu tiếng nói không bị mai một thì những văn hóa khác sẽ không bị biến mất. Và trước bị phong kiến phương bắc đô hộ thì nước ta đã có một nền văn hóa riêng của mình như thờ cúng tổ tiên, nhuộm răng ăn trầu, văn hóa trên trống đồng Đông Sơn,.... Khi bị đô hộ thì nhân dân ta đã có ý thức dân tộc, về cội nguộn của mình , mặc dù bị đô hộ và người phương bắc đã hòa huyết với người của ta 1000 năm nhưng những văn hóa truyền thống ấy không biến mất mà vẫn còn được lưu truyền đến ngày nay. Do đó những chính sách đồng hóa của phong kiến phương Bắc bị thất bại, có một viên đô hộ sứ từng nói rằng "dân xứ ấy rất khó trị".
C
15 tháng 1 2020
\(\frac{x}{2000}+\frac{x+2}{2002}+\frac{x+4}{2004}+....+\frac{x+12}{2012}=7\)
\(\Leftrightarrow\left(\frac{x}{2000}-1\right)+\left(\frac{x+2}{2002}-1\right)+\left(\frac{x+4}{2004}-1\right)+......+\left(\frac{x+12}{2012}-1\right)=0\)
\(\Leftrightarrow\frac{x-2000}{2000}+\frac{x-2000}{2002}+\frac{x-2000}{2004}+.....+\frac{x-2000}{2012}=0\)
\(\Leftrightarrow\left(x-2000\right)\left(\frac{1}{2000}+\frac{1}{2002}+\frac{1}{2004}+....+\frac{1}{2012}\right)=0\)
Dễ thấy \(\frac{1}{2000}+\frac{1}{2002}+....+\frac{1}{2012}>0\Rightarrow x-2000=0\Rightarrow x=2000\)
C
15 tháng 1 2020
\(\frac{x+1}{15}+\frac{x+2}{7}+\frac{x+4}{4}+6=0\)
\(\Leftrightarrow\left(\frac{x+1}{15}+1\right)+\left(\frac{x+2}{7}+2\right)+\left(\frac{x+4}{4}+3\right)=0\)
\(\Leftrightarrow\frac{x+16}{15}+\frac{x+16}{7}+\frac{x+16}{4}=0\)
\(\Leftrightarrow\left(x+16\right)\left(\frac{1}{15}+\frac{1}{7}+\frac{1}{4}\right)=0\)
Dễ thấy \(\frac{1}{4}+\frac{1}{7}+\frac{1}{15}>0\Rightarrow x+16=0\Rightarrow x=-16\)
xy−2x−3y=5xy−2x−3y=5
⇔xy−3y−2x=5⇔xy−3y−2x=5
⇔y(x−3)−2x+6=11⇔y(x−3)−2x+6=11
⇔y(x−3)−(2x−6)=11⇔y(x−3)−(2x−6)=11
⇔y(x−3)−2(x−3)=11⇔y(x−3)−2(x−3)=11
⇔(y−2)(x−3)=11
<=> Ta có{{y−2x−3∈Ư(11)={±1;±11}
Ta có bảng sau:
Vậy có 4 cặp số nguyên x , y thỏa mãn: (−8;1);(2;−9);(4;13);(14;3)