Nếu phương trình 3x^2+5y =28 có nghiệm nguyên (x ; y) thì x chia cho 5 có số dư là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



3x2 + 5y = 28
=> 3x2 ≤ 28
=> x2 ≤ 9
=> x ≤ 3
Xét x = 0 => 5y = 28 ( loại )
Xét x = 1 => 3 + 5y = 28 => y = 5
Vì 1 chia 5 dư 1 => x0 chia 5 dư 1


pt: \(9.3^x+5y=28\Leftrightarrow10.3^x+5y-3^x=28\)
Ta thấy: \(10.3^x+5y⋮5\)Mà 28 chia 5 dư 3 => \(3^x\):5 dư 3
xét các chữ số tận cùng của \(3^x\)là: 1,3,7,9 => \(3^x\)phải có tận cùng là 3 => x=4k+1
đoạn sau tự giải quyết nốt nhé!

bn tham khảo câu này nha https://h.vn/hoi-dap/question/79049.html
chúc bn học tốt.tk mk nha

x2 + 2y2 + 3xy + 3x + 5y = 15
Û (x +y +z )(x + 2y +1)
đúng không???

a)
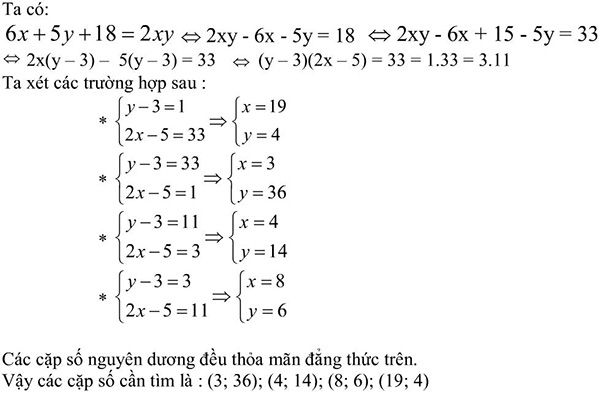
b)
Nhận thấy: x phải là số lẻ. Vì nếu x là số chẵn thì 3x^2 sẽ là số chẵn => 3x^2-4y^2 là số chẵn trong khi 13 là số lẻ
x là số lẻ => x có dạng x= 2k+1 với k thuộc Z
thay x=2k+1 vào phương trình ta có:
3(4k^2+4k+1) - 4y^2 = 13
<=> 6k^2+6k-2y^2=5
<=> 6k(k+1) = 5+2y^2
Dễ thấy vế trái là số chẵn trong khi vế phải là số lẻ => phương trình không có nghiệm nguyên => dpcm
Lam nhanh ho mk voi mk rat gap