Điểm thi môn Toán của các bạn trong lớp được cho trong bảng sau:
| Điểm | 0 | 5 | 6 | 7 | 10 |
| Tần số | 1 | 10 | 20 | 10 | 1 |
Tìm khoảng biến thiên của mẫu số liệu trên. Có nên dùng đại lượng này để đo độ phân tán của mẫu số liệu trên không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nhận xét: Số trung bình cộng điểm thi Toán của lớp 10A cao hơn lớp 10B nên có thể nói lớp 10A có kết quả thi môn Toán tốt hơn lớp 10B.

Chọn A.
Bảng phân bố tần số - tần suất
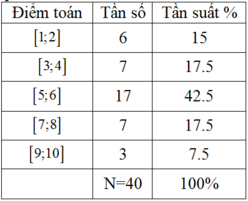
Dựa vào bảng trên ta thấy lớp 3 có tần số và tần suất cao nhất; lớp 5 có tần số; tần suất thấp nhất.
Lớp 2 và 4 có cùng tần số và tần suất.

a) * Lớp 10C:

* Lớp 10D:

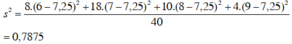
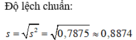
b) Kết quả lớp 10D có độ lệch chuẩn nhỏ hơn kết quả lớp 10C nên kết quả lớp 10D đồng đều hơn.

a) Lớp 7A có 3.10=30 học sinh
b)
| Số điểm(x) | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Tần số (n) | 1 | 2 | 3 | 4 | 8 | 6 | 4 | 2 |
- Số trung bình cộng của dấu hiệu là:
\(\overline{X}=\dfrac{3.1+4.2+5.3+6.4+7.8+8.6+9.4+10.2}{30}=7\)
- Mốt của dấu hiệu là 7
a) Lớp 7A có 30 bạn học sinh
b)
| Số điểm(x) | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Tần số (n) | 1 | 2 | 3 | 4 | 8 | 6 | 4 | 2 |
- Số trung bình cộng của dấu hiệu là:
¯¯¯¯¯X=3.1+4.2+5.3+6.4+7.8+8.6+9.4+10.2:30=7
- Mốt của dấu hiệu là 7

Số bạn trên điểm 7 bằng số phần bạn trong lớp là:
1/5 + 2/5 + 1/6 = 23/30 ( bạn )
Đáp số: 23/30 bạn

Gọi x là tần số của điểm 4 (x > 0; x ∈ N)
Số học sinh của lớp:
2 + x + 10 + 12 + 7 + 6 + 4 + 1 = 42 + x
Vì điểm trung bình bằng 6,06 nên:
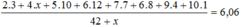
⇔ 6 + 4x + 50 + 72 + 49 + 48 + 36 + 10 = 6,06(42 + x)
⇔ 271 + 4x = 254,52 + 6,06x ⇔ 16,48 = 2,06x
⇔ x = 8 (thỏa mãn điều kiện đặt ra)
Vậy ta có kết quả điền vào như sau:
| Điểm (x) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Tần số (f) | 0 | 0 | 2 | 8 | 10 | 12 | 7 | 6 | 4 | 1 | N = 50 |
Điểm thi thấp nhất là 00 , cao nhất là 1010 . Do đó, khoảng biến thiên là 10-0=1010−0=10.
Hầu hết các bạn trong lớp có điểm 5,6,75,6,7 vì vậy dùng khoảng biến thiên để đo độ phân tán của dãy số liệu này sẽ không hợp lí.