Cho tam giác ABC vuông tại A, lấy điểm D thuộc cạnh huyền BC (D không trùng B và C) . Gọi M, N lần lượt đối xứng với D qua AB, AC. Gọi I là giao điểm của MD với AB, K là giao điểm của ND với AC.
a) Chứng minh tứ giác AIDK là hình chữ nhật.
b) Chứng minh M đối xứng với N qua A.
c) Tìm vị trí của D trên cạnh BC sao cho CM đi qua trung điểm của IK.

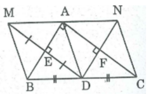
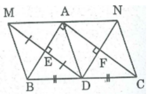
a) Tứ giác AIDK là hình chữ nhật
b) M đối xứng với N qua A
c) Để CM đi qua trung điểm của IK thì D là trung điểm cạnh BC
Giải thích các bước giải:
a)
M đối xứng với D qua AB (gt)
I là giao điểm của MD với AB (gt)
→MI=ID,MD⊥AB→MI=ID,MD⊥AB tại I
Tương tự: NK=KD,ND⊥ACNK=KD,ND⊥AC tại K
Xet tứ giác AIDK:
ˆIAK=90o(AB⊥AC)ˆAID=90o(DI⊥AB)ˆAKD=90o(DK⊥AC)IAK^=90o(AB⊥AC)AID^=90o(DI⊥AB)AKD^=90o(DK⊥AC)
→→ Tứ giác AIDK là hình chữ nhật (tứ giác có 3 góc vuông)
→→ 2 đường chéo AD và IK cắt nhau tại trung điểm mỗi đường là điểm O
→ID//AK,ID=AK;IA//DK,IA=DK→ID//AK,ID=AK;IA//DK,IA=DK
b)
Xét tứ giác MIKA:
MI//AK(ID//AK)MI=AK(=ID)MI//AK(ID//AK)MI=AK(=ID)
→→ Tứ giác MIKA là hình bình hành (2 cạnh đối song song và bằng nhau)
→MA//IK,MA=IK→MA//IK,MA=IK
Xét tứ giác AIKN:
IA//KN(IA//DK)IA=KN(=DK)IA//KN(IA//DK)IA=KN(=DK)
→→ Tứ giác AIKN là hình bình hành (2 cạnh đối song song và bằng nhau)
→AN//IK,AN=IK→AN//IK,AN=IK
→→ M, A, N thẳng hàng
→MA=AN→MA=AN
→→ M đối xứng với N qua A
c)
Để CM đi qua trung điểm của IK
Hay CM đi qua điểm O
→→ CM cắt AD tại trung điểm O của mỗi đường
→→ Tứ giác CAMD là hình bình hành (2 đường chéo cắt nhau tại trung điểm mỗi đường)
→MD=AC→2ID=AC→ID=12AC→MD=AC→2ID=AC→ID=12AC
Mà ID//AC(ID//AK)ID//AC(ID//AK)
→→ ID là đường trung bình của △ABC△ABC
→→ D là trung điểm của BC
Vậy để CM đi qua trung điểm của IK thì D là trung điểm cạnh BC