Tìm x biết
(5-2x)^3-27=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
13 tháng 7 2017
a) (x – 45).27 = 0 ó x – 45 = 0 ó x = 45
b) 45.(2x – 4).13 = 0 ó 2x – 4 = 0 ó 2x – 4 = 0 ó 2x = 4 ó x = 2
c) (x – 3).(x – 5) = 0
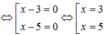
Vậy tập nghiệm của phương trình là S = {3;5}
BT
1
DT
5 tháng 8 2016
1) \(4x^2-25-\left(2x-5\right)\left(2x+7\right)=0\)
\(\Leftrightarrow\left(2x-5\right)\left(2x+5\right)-\left(2x-5\right)\left(2x+7\right)=0\)
\(\Leftrightarrow\left(2x-5\right)\left(2x+5-2x-7\right)=0\)
\(\Leftrightarrow\left(2x-5\right).-2=0\)
\(\Leftrightarrow-4x+10=0\)
\(\Leftrightarrow-4x=-10\)
\(\Leftrightarrow x=\frac{5}{2}.\)
Vậy \(S=\left\{\frac{5}{2}\right\}\)
2)\(x^3+27+\left(x+3\right)\left(x-9\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-3x+9\right)+\left(x+3\right)\left(x-9\right)=0\)
\(\Leftrightarrow\left(x+3\right).\left(x^2-3x+9+x-9\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-2x\right)=0\)
\(\Leftrightarrow\left(x+3\right).x.\left(x-2\right)=0\)
\(\Leftrightarrow x+3=0\)hoặc \(x=0\)hoặc \(x-2=0\)
\(\Leftrightarrow x=-3\)hoặc \(x=0\)hoặc \(x=2\)
Vậy \(S=\left\{-3;0;2\right\}\)
CM
11 tháng 9 2019
a) x = 1; x = - 1 3 b) x = 2.
c) x = 3; x = -2. d) x = -3; x = 0; x = 2.
KM
16 tháng 8 2019
a) \(\left(2x+\frac{3}{5}\right)^2-\frac{9}{25}=0\)
\(\left(2x+\frac{3}{5}\right)^2=\frac{9}{25}\)
\(\left(2x+\frac{3}{5}\right)^2=\left(\frac{3}{5}\right)^2\)
\(=>2x+\frac{3}{5}=\frac{3}{5}\)
\(2x=\frac{3}{5}-\frac{3}{5}\)
\(2x=0\)
\(x=0:2\)
\(x=0\)
KM
16 tháng 8 2019
b) \(\left(3x-1\right).\left(-\frac{1}{2x}+5\right)=0\)
=> \(\left(3x-1\right)=0\)hoặc \(\left(-\frac{1}{2x}+5\right)=0\)hoặc \(\left(3x-1\right)\)và\(\left(-\frac{1}{2x}+5\right)\)cùng bằng 0.
\(\orbr{\begin{cases}3x-1=0\\-\frac{1}{2x}+5=0\end{cases}}=>\orbr{\begin{cases}3x=1\\-\frac{1}{2x}=-5\end{cases}}=>\orbr{\begin{cases}x\in\varnothing\\2x=\frac{1}{5}\end{cases}}=>x=\frac{1}{5}:2=>x=\frac{1}{10}\)
MT
5 tháng 6 2015
(2x-5)3+27(x-1)3+(8-5x)3=0
<=>(2x-5)3+33(x-1)3+(8-5x)3=0
<=>(2x-5)3+(3x-3)3+(8-5x)3=0
Đặt a=2x-5
b=3x-3
c=8-5x
=>a+b+c=2x-5+3x-3+8-5x=0
và a3+b3+c3=0(theo đề bài ta có)
ta có (a+b+c)3=(a+b)3+3(a+b)2c+3(a+b)c2+c3
=a3+b3+c3+3a2b+3ab2+3(a+b)2c+3(a+b)c2
=a3+b3+c3+3ab(a+b)+3(a+b)c(a+b+c)
=a3+b3+c3+3(a+b)(ab+c(a+b+c)
=a3+b3+c3+3(a+b)(ab+ca+cb+c2)
=a3+b3+c3+3(a+b)[a(b+c)+c(b+c)]
=a3+b3+c3+3(a+b)(b+c)(c+a)
Mà a+b+c=0 và a3+b3+c3=0 nên
3(a+b)(b+c)(c+a)=0
<=>(a+b)(b+c)(c+a)=0
<=>(2x-5+3x-3)(3x-3+8-5x)(8-5x+2x-5)=0
<=>(5x-8)(-2x+5)(-3x-3)=0
<=>5x-8=0 hoặc -2x+5=0 hoặc -3x-3=0
<=> x =8/5 hoặc x =5/2 hoặc x =-1
DM
0
NT
6
TH
3 tháng 7 2019
a, \(27\left(x-45\right)=0\)
\(\Leftrightarrow x-45=0\)
\(\Leftrightarrow x=45\)
b, \(\left(x-3\right)\left(x-5\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-3=0\\x-5=0\end{cases}\Rightarrow}\orbr{\begin{cases}x=3\\x=5\end{cases}}\)
c, \(\left(2x-6\right)\left(x+3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}2x-6=0\\x+3=0\end{cases}\Rightarrow}\orbr{\begin{cases}2x=6\\x=-3\end{cases}\Rightarrow\orbr{\begin{cases}x=3\\x=-3\end{cases}}}\)
3 tháng 7 2019
\(a;27.\left(x-45\right)=0\Leftrightarrow x-45=0\Rightarrow x=45\)
\(b;\left(x-3\right)\left(x-5\right)=0\Leftrightarrow\orbr{\begin{cases}x-3=0\\x-5=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=5\end{cases}}}\)
\(c;\left(2x-6\right)\left(x+3\right)=0\Leftrightarrow\orbr{\begin{cases}2x-6=0\\x+3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=-3\end{cases}}}\)
(5-2x)^3=0+27
(5-2x)^3=27
(5-2x)^3=3^3
5-2x=3
2x=5-3
2x=2
x=2:2
x=1
như bài lớp 6