Có 31 học sinh dự thi môn toán.Bộ đề thi gồm 5 câu hỏi khác nhau ,moi bạn học sinh sẽ bốc thăm chọn 3 câu trong 5 câu hỏi để làm thành đề thi của mình .Chứng minh rằng có ít nhất bốn học sinh cùng một đề
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 12 2015
chẳng có ai trả lời hết ,vậy thì mình trả lời luôn cho:
Ta có :
_Có 5 cách chọn câu số 1 cho đề thi
_Có 4 cách chọn câu số 2 cho đề thi
_Có 3 cách chọn câu số 3 cho đề thi
Số đề thi được lập là :
5 x 4 x 3 =60 (đề thi)
Nhưng nếu làm như vậy thì mỗi đề thi được tính đến 6 lần , chẳng hạn đề thi gồm các câu (1,2,3)sẽ trùng với các đề thi :(1,3,2);(2,1,3;(2,3,1);(3,1,2);(3,2,1)
Thực sự số đề thi là :
60 : 6 =10 (đề thi )
Ta có :31:10=3
Vậy có ít nhất 4 học sinh làm cùng đề thi
CM
10 tháng 1 2018
10 bộ đề thi mỗi đề thi là 10 câu tương ứng với 10 x10=100 (câu hỏi)
Mỗi em 3 câu, tình huống xấu nhất là em 3 có số câu trùng nhau thì hết x100=300 (em)
Thừa ra số em là: 370-300=70 (em)
70 em này sẽ bốc vào các câu mà đã có ít nhất 3 người đã bốc. Vậy sẽ có 4 người có số câu trùng nhau.
CM
26 tháng 7 2018
10 bộ đề thi mỗi đề thi là 10 câu tương ứng với 10 x10=100 (câu hỏi) Mỗi em 3 câu, tình huống xấu nhất là em 3 có số câu trùng nhau thì hết x100=300 (em) Thừa ra số em là: 370-300=70 (em) 70 em này sẽ bốc vào các câu mà đã có ít nhất 3 người đã bốc. Vậy sẽ có 4 người có số câu trùng nhau
HT
7 tháng 2 2021
Ít nhất 1 câu hình học, nhiều nhất là 3 câu hình học, bởi giới hạn chỉ được bốc 3 câu hỏi
Khong gian mau: \(n\left(\Omega\right)=C^3_{15}\)
TH1: Bốc 1 câu hình học và 2 câu đại số
\(C^1_5.C^2_{10}\)
TH2: Bốc 2 câu hình học và 1 câu đại số
\(C^2_5.C^1_{10}\)
TH3: Bốc 3 câu hình học
\(C^3_5\)
\(\Rightarrow C^1_5.C^2_{10}+C^2_5.C^1_{10}+C^3_5=..\)
\(p\left(A\right)=\dfrac{C^1_5.C^2_{10}+C^2_5.C^1_{10}+C^3_5}{C^3_{15}}=...\)
7 tháng 2 2021
Ω: "Chọn 3 câu hỏi từ 15 câu."
⇒ n(Ω) = \(C^3_{15}=455\)
A: "Chọn được ít nhất 1 câu hỏi Hình học."
⇒ \(\overline{A}\): "Không chọn được câu Hình học nào."
\(\Rightarrow n\left(\overline{A}\right)=C^3_{10}=120\)
\(\Rightarrow P\left(\overline{A}\right)=\dfrac{120}{455}=\dfrac{24}{91}\)
\(\Rightarrow P\left(A\right)=1-P\left(\overline{A}\right)=\dfrac{67}{91}\)
Bạn tham khảo nhé!
CM
4 tháng 8 2019
Đáp án A
Ta xét 2 trường hợp:
TH1: Đề thi có 9 câu hỏi nằm trong 25 câu mà học sinh nắm được ⇒ P 1 = C 25 9 . C 5 1 C 30 10
TH2: Đề thi có 10 câu hỏi nằm trong 25 câu mà học sinh nắm được ⇒ P 2 = C 25 10 C 30 10
Vậy xác suất cần tính là P = P 1 + P 2 = 0 , 449
CM
7 tháng 2 2019
Đáp án A
Ta xét 2 trường hợp
TH1:
Đề thi có 9 câu hỏi nằm trong 25 câu mà học sinh nắm được
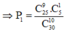
TH2:
Đề thi có 10 câu hỏi nằm trong 25 câu mà học sinh nắm được
Vậy xác suất cần tính là
trả lời deeeee
Gọi 5 câu hỏi lần lượt là a, b, c, d, e
Chọn 3 trong 5 câu hỏi, ta có số đề khác nhau là :
abc, abd, abe, acd, ace, ade
bcd, bce, bde
cde
Vậy có 10 đề khác nhau
31 : 10 dư 1
Nên ít nhất có 1 trường hợp 4 học sinh cùng đề