Tìm m để có hai điểm cực trị tại thỏa mãn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
y ' = 3 x 2 - 6 x + m .
Hàm số có cực trị khi y' = 0 có hai nghiệm phân biệt :


Chọn D.
Ta có: ![]()
Để hàm số có hai cực trị x1, x2 thì phương trình (1) có hai nghiệm phân biệt.
Khi đó: ![]()
Mà theo yêu cầu bài toán x1, x2 thỏa mãn:
x
1
2
+
x
2
2
=
6
![]()
Mặt khác theo Vi-et ta có: 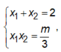
thay vào (2) ta được ![]() thỏa mãn điều kiện (*).
thỏa mãn điều kiện (*).
Vậy m = -3.
y'=3x2−6x+m.y'=3x2-6x+m.
Hàm số có hai cực trị khi y' = 0 có hai nghiệm phân biệt :