NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
18 tháng 7 2017
Chọn A
y ' = 3 x 2 - 6 x + m .
Hàm số có cực trị khi y' = 0 có hai nghiệm phân biệt :
CM
9 tháng 3 2018
Chọn D.
Ta có: 
Để hàm số có hai cực trị x1, x2 thì phương trình (1) có hai nghiệm phân biệt.
Khi đó: 
Mà theo yêu cầu bài toán x1, x2 thỏa mãn:
x
1
2
+
x
2
2
=
6
Mặt khác theo Vi-et ta có: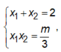 
thay vào (2) ta được 
thỏa mãn điều kiện (*).
Vậy m = -3.
CM
15 tháng 6 2018
Chọn D
D = ℝ
Phương trình y ' = 0 luôn có hai nghiệm phân biệt x 1 , x 2 và y ' đổi dấu khi x chạy qua x 1 , x 2
nên hàm số đạt cực trị tại x 1 , x 2 .
Phương pháp trắc nghiệm:
Bước 1: Giải phương trình bậc hai :
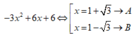
Bước 2: Tính A 2 + B 2 = 8
CM
4 tháng 5 2018
Đáp án A
Ghi nhớ: Nếu hàm số 
liên tục trên đoạn 
và 
thì phương trình 
có ít nhất một nghiệm nằm trong khoảng 
.
CM
16 tháng 3 2018
y ' = - 3 x 2 + 2 ( 2 m + 1 ) x - m 2 + 3 m - 2
Để hàm số đã cho có cực đại, cực tiểu nằm về hai phía so với trục tung khi và chỉ khi phương trình y’ = 0 có hai nghiệm x 1 , x 2 trái dấu.
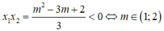
Chọn A
CM
7 tháng 8 2019
Ta có: y ' = 3 x 2 - 6 m x + 3 m 2 - 3
Để đồ thị hàm số đã cho có 2 điểm cực trị khi và chỉ khi phương trình y’ = 0 có 2 nghiệm phân biệt và y’ đổi dấu qua các nghiệm đó.
y' = 3x^2 - 6mx + 3m^2 - 3
⇔ Δ ' = 9 m 2 - 9 m 2 + 9 = 9 > 0
Do đó, hàm số đã cho có 2 điểm cực trị x 1 , x 2 là nghiệm phương trình y’ = 0.
Áp dụng hệ thức Vi-et ta có:
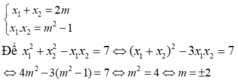
Chọn D.
CM
1 tháng 11 2017
+ Ta có hàm số g(x) = x 3 - 3 x 2 + 2 = m là hàm số chẵn nên đồ thị nhận trục Oy làm trục đối xứng.
+ Khi x≥ 0 ; g(x) = x3- 3x2+ 2
Do đó; đồ thị hàm số g(x) = x 3 - 3 x 2 + 2 có dạng như hình vẽ.
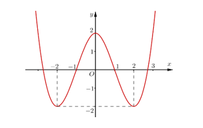
+ Dựa vào đồ thị suy ra phương trình x 3 - 3 x 2 + 2 = m có nhiều nghiệm thực nhất khi và chỉ khi -2< m< 2.
Chọn C.
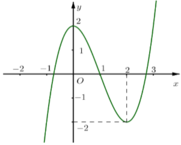
y'=3x2−6x+m.y'=3x2-6x+m.
Hàm số có hai cực trị khi y' = 0 có hai nghiệm phân biệt :