Bài 34 (trang 19 SGK Toán 9 Tập 1)
Rút gọn các biểu thức sau:
a) $ab^2.\sqrt{\dfrac{3}{a^2b^4}}$ với $a<0$,$b \ne 0$ ; b) $\sqrt{\dfrac{27(a-3)^2}{48}}$ với $a>3$ ;
c) $\sqrt{\dfrac{9+12a+4a^2}{b^2}}$ với $a \ge -1,5$ và $b<0$ ; d) $(a-b).\sqrt{\dfrac{ab}{(a-b)^2}}$ với $a<b<0$.



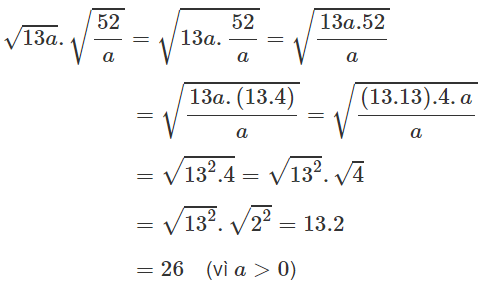

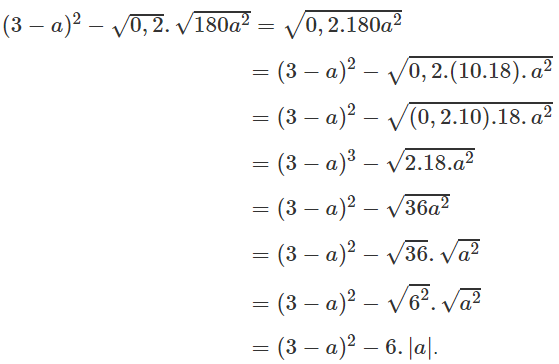
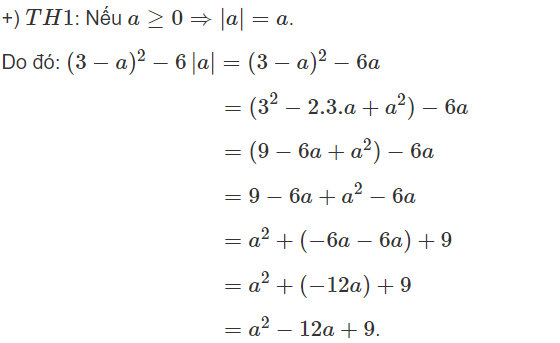
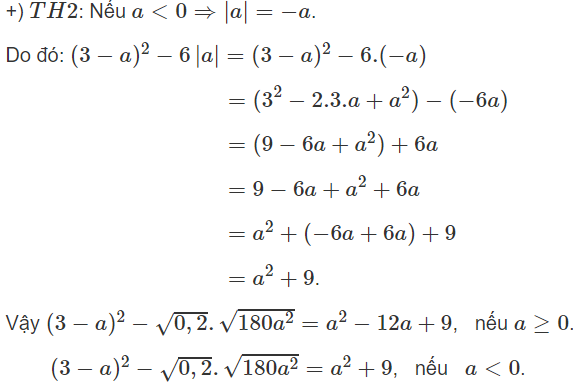
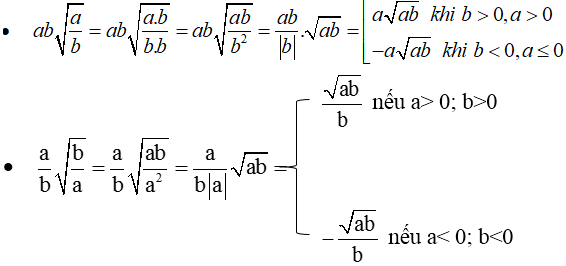

a) ab2.√3a2b4=ab2.√3√a2b4ab2.3a2b4=ab2.3a2b4
=ab2.√3√a2.√b4=ab2.√3|a|.|b2|=ab2.3a2.b4=ab2.3|a|.|b2|
=ab2.√3(−a).b2=ab2.3(−a).b2 (Do a<0a<0 nên |a|=−a|a|=−a và b≠0b≠0 nên b2>0b2>0 ⇒⇒ ∣∣b2∣∣=b2|b2|=b2)
=−√3=−3.
b) √27(a−3)248=√9(a−3)21627(a−3)248=9(a−3)216
=√9.√(a−3)2√16=3.|a−3|4=9.(a−3)216=3.|a−3|4
=3(a−3)4=3(a−3)4.
(Do a>3a>3 nên |a−3|=a−3|a−3|=a−3)
c) √9+12a+4a2b2=√32+2.3.2a+(2a)2√b29+12a+4a2b2=32+2.3.2a+(2a)2b2
=√(3+2a)2√b2=|3+2a||b|=(3+2a)2b2=|3+2a||b|
=3+2a−b=−2a+3b=3+2a−b=−2a+3b.
(Do a≥−1,5a≥−1,5 ⇒⇒ 3+2a≥03+2a≥0 nên |3+2a|=3+2a|3+2a|=3+2a và b<0b<0 nên |b|=−b|b|=−b)
d) (a−b).√ab(a−b)2=(a−b).√ab√(a−b)2(a−b).ab(a−b)2=(a−b).ab(a−b)2
=(a−b).√ab|a−b|=(a−b).√ab−(a−b)=(a−b).ab|a−b|=(a−b).ab−(a−b)
=−√ab=−ab.
(Do a<b<0a<b<0 nên |a−b|=−(a−b)|a−b|=−(a−b) và ab>0ab>0)
a) ab2.√3a2b4=ab2.√3√a2b4ab2.3a2b4=ab2.3a2b4
=ab2.√3√a2.√b4=ab2.√3|a|.|b2|=ab2.3a2.b4=ab2.3|a|.|b2|
=ab2.√3(−a).b2=ab2.3(−a).b2 (Do a<0a<0 nên |a|=−a|a|=−a và b≠0b≠0 nên b2>0b2>0 ⇒⇒ ∣∣b2∣∣=b2|b2|=b2)
=−√3=−3.
b) √27(a−3)248=√9(a−3)21627(a−3)248=9(a−3)216
=√9.√(a−3)2√16=3.|a−3|4=9.(a−3)216=3.|a−3|4
=3(a−3)4=3(a−3)4.
(Do a>3a>3 nên |a−3|=a−3|a−3|=a−3)
c) √9+12a+4a2b2=√32+2.3.2a+(2a)2√b29+12a+4a2b2=32+2.3.2a+(2a)2b2
=√(3+2a)2√b2=|3+2a||b|=(3+2a)2b2=|3+2a||b|
=3+2a−b=−2a+3b=3+2a−b=−2a+3b.
(Do a≥−1,5a≥−1,5 ⇒⇒ 3+2a≥03+2a≥0 nên |3+2a|=3+2a|3+2a|=3+2a và b<0b<0 nên |b|=−b|b|=−b)
d) (a−b).√ab(a−b)2=(a−b).√ab√(a−b)2(a−b).ab(a−b)2=(a−b).ab(a−b)2
=(a−b).√ab|a−b|=(a−b).√ab−(a−b)=(a−b).ab|a−b|=(a−b).ab−(a−b)
=−√ab=−ab.
(Do a<b<0a<b<0 nên |a−b|=−(a−b)|a−b|=−(a−b) và ab>0ab>0)